Brownian excursion
Brownian excursion process
The limiting process of a Bernoulli excursion. If  is a Bernoulli excursion, and if
is a Bernoulli excursion, and if  , then the finite-dimensional distributions of the process
, then the finite-dimensional distributions of the process 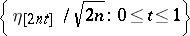 converge to the corresponding finite-dimensional distributions of a process
converge to the corresponding finite-dimensional distributions of a process  which is called a Brownian excursion (process). The Brownian excursion process
which is called a Brownian excursion (process). The Brownian excursion process  is a Markov process for which
is a Markov process for which 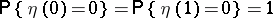 and
and 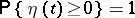 for
for  . If
. If  , then
, then  has a density function
has a density function  . Obviously,
. Obviously, 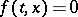 for
for 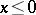 . If
. If 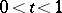 and
and  , then
, then
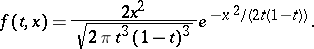 |
If 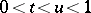 , then the random variables
, then the random variables  and
and  have a joint density function
have a joint density function  . One finds that
. One finds that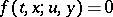 if
if 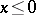 or
or  . If
. If 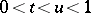 and
and 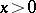 ,
,  , then
, then
 |
 |
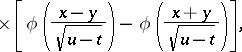 |
where
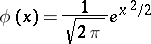 |
is the normal density function (cf. Normal distribution; Density of a probability distribution). Since 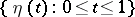 is a Markov process, the density functions
is a Markov process, the density functions  and
and 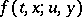 completely determine its finite-dimensional distributions. For various properties of the Brownian excursion process, see [a3], [a1], [a4].
completely determine its finite-dimensional distributions. For various properties of the Brownian excursion process, see [a3], [a1], [a4].
The distributions of various functionals of the Brownian excursion  frequently appear in probability theory. In particular, many limit distributions of the Bernoulli excursion
frequently appear in probability theory. In particular, many limit distributions of the Bernoulli excursion 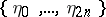 can be expressed simply as the distributions of certain functionals of the Brownian excursion. For example, if
can be expressed simply as the distributions of certain functionals of the Brownian excursion. For example, if 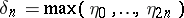 , then
, then
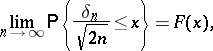 |
where
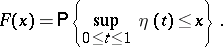 |
Explicitly,
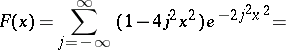 |
 |
for  and
and 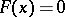 for
for 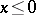 .
.
References
| [a1] | K.L. Chung, "Excursions in Brownian Motion" Arkiv für Math. , 14 (1976) pp. 157–179 |
| [a2] | K. Itô, H.P. McKean, "Diffusion processes and their sample paths" , Springer (1965) |
| [a3] | P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965) (Edition: Second) |
| [a4] | L. Takács, "A Bernoulli excursion and its various applications" Adv. in Probability , 23 (1991) pp. 557–585 |
Brownian excursion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brownian_excursion&oldid=15228