Friedrichs inequality
An inequality of the form
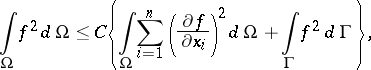 | (1) |
where  is a bounded domain of points
is a bounded domain of points  in an
in an  -dimensional Euclidean space with an
-dimensional Euclidean space with an  -dimensional boundary
-dimensional boundary  satisfying a local Lipschitz condition, and the function
satisfying a local Lipschitz condition, and the function  (a Sobolev space).
(a Sobolev space).
The right-hand side of the Friedrichs inequality gives an equivalent norm in  . Using another equivalent norm in
. Using another equivalent norm in  , one obtains (see [2]) a modification of the Friedrichs inequality of the form
, one obtains (see [2]) a modification of the Friedrichs inequality of the form
 | (2) |
There are generalizations (see [3]–[5]) of the Friedrichs inequality to weighted spaces (see Weighted space; Imbedding theorems). Suppose that  and that the numbers
and that the numbers  ,
,  and
and  are real, with
are real, with  being a natural number and
being a natural number and  . One says that
. One says that  if the norm
if the norm
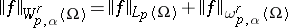 |
is finite, where
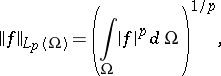 |
 |
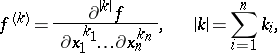 |
and 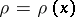 is distance function from
is distance function from  to
to 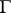 .
.
Suppose that  is a natural number such that
is a natural number such that
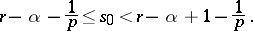 |
Then, if  ,
, 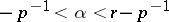 ,
,  , for
, for  the following inequality holds:
the following inequality holds:
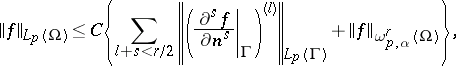 |
where  is the derivative of order
is the derivative of order  with respect to the interior normal to
with respect to the interior normal to  at the points of
at the points of 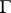 .
.
One can also obtain an inequality of the type (2), which has in the simplest case the form
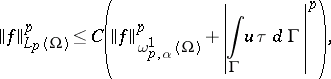 |
where
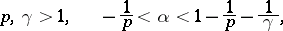 |
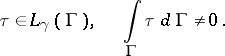 |
The constant  is independent of
is independent of  throughout.
throughout.
The inequality is named after K.O. Friedrichs, who obtained it for  ,
, 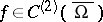 (see [1]).
(see [1]).
References
| [1] | K.O. Friedrichs, "Eine invariante Formulierung des Newtonschen Gravititationsgesetzes und des Grenzüberganges vom Einsteinschen zum Newtonschen Gesetz" Math. Ann. , 98 (1927) pp. 566–575 |
| [2] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [3] | S.M. Nikol'skii, P.I. Lizorkin, "On some inequalities for weight-class functions and boundary-value problems with a strong degeneracy at the boundary" Soviet Math. Dokl. , 5 (1964) pp. 1535–1539 Dokl. Akad. Nauk SSSR , 159 : 3 (1964) pp. 512–515 |
| [4] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [5] | D.F. Kalinichenko, "Some properties of functions in the spaces 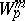 and and 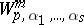 " Mat. Sb. , 64 : 3 (1964) pp. 436–457 (In Russian) " Mat. Sb. , 64 : 3 (1964) pp. 436–457 (In Russian) |
| [6] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [7] | L. Nirenberg, "On elliptic partial differential equations" Ann. Scuola Norm. Sup. Pisa Ser. 3 , 13 : 2 (1959) pp. 115–162 |
| [8] | L. Sandgren, "A vibration problem" Medd. Lunds Univ. Mat. Sem. , 13 (1955) pp. 1–84 |
Friedrichs inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Friedrichs_inequality&oldid=15223