A statistical test used for testing a simple non-parametric hypothesis 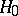 (cf. Non-parametric methods in statistics), according to which independent identically-distributed random variables
(cf. Non-parametric methods in statistics), according to which independent identically-distributed random variables 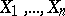 have a given continuous distribution function
have a given continuous distribution function 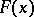 , against the alternatives:
, against the alternatives:
where 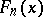 is the empirical distribution function constructed with respect to the sample
is the empirical distribution function constructed with respect to the sample 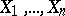 and
and 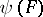 ,
, 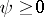 , is a weight function. If
, is a weight function. If
where  is any fixed number from the interval
is any fixed number from the interval 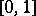 , then the Rényi test, which was intended for testing
, then the Rényi test, which was intended for testing 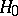 against the alternatives
against the alternatives 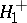 ,
, 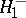 ,
, 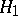 , is based on the Rényi statistics
, is based on the Rényi statistics
where 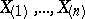 are the members of the series of order statistics
are the members of the series of order statistics
constructed with respect to the observations 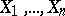 .
.
The statistics 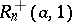 and
and 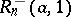 satisfy the same probability law and, if
satisfy the same probability law and, if 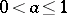 , then
, then
 | (1) |
 | (2) |
where 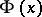 is the distribution function of the standard normal law (cf. Normal distribution) and
is the distribution function of the standard normal law (cf. Normal distribution) and 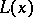 is the Rényi distribution function,
is the Rényi distribution function,
If 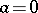 , then
, then
It follows from (1) and (2) that for larger values of  the following approximate values may be used to calculate the
the following approximate values may be used to calculate the 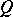 -percent critical values
-percent critical values 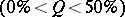 for the statistics
for the statistics 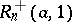 and
and 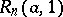 :
:
respectively, where 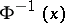 and
and 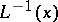 are the inverse functions to
are the inverse functions to 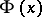 and
and 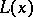 , respectively. This means that if
, respectively. This means that if 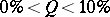 , then
, then 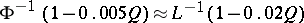 .
.
Furthermore, if 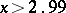 , then it is advisable to use the approximate equation
, then it is advisable to use the approximate equation
when calculating the values of the Rényi distribution function 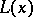 ; its degree of error does not exceed
; its degree of error does not exceed 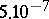 .
.
In addition to the Rényi test discused here, there are also similar tests, corresponding to the weight function
where  is any fixed number from the interval
is any fixed number from the interval 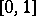 .
.
References
| [1] | A. Rényi, "On the theory of order statistics" Acta Math. Acad. Sci. Hungar. , 4 (1953) pp. 191–231 |
| [2] | J. Hájek, Z. Sidák, "Theory of rank tests" , Acad. Press (1967) |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
How to Cite This Entry:
Rényi test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=R%C3%A9nyi_test&oldid=15214
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article (cf. Non-parametric methods in statistics), according to which independent identically-distributed random variables
(cf. Non-parametric methods in statistics), according to which independent identically-distributed random variables 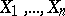 have a given continuous distribution function
have a given continuous distribution function 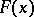 , against the alternatives:
, against the alternatives:
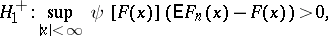
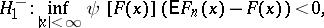
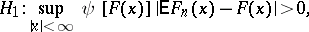
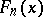 is the empirical distribution function constructed with respect to the sample
is the empirical distribution function constructed with respect to the sample 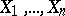 and
and 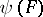 ,
, 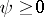 , is a weight function. If
, is a weight function. If
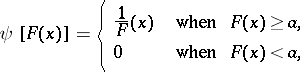
 is any fixed number from the interval
is any fixed number from the interval 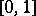 , then the Rényi test, which was intended for testing
, then the Rényi test, which was intended for testing 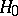 against the alternatives
against the alternatives 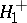 ,
, 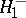 ,
, 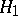 , is based on the Rényi statistics
, is based on the Rényi statistics
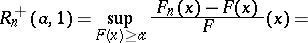
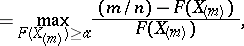
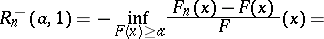
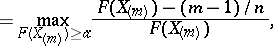
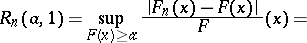
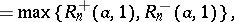
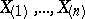 are the members of the series of order statistics
are the members of the series of order statistics
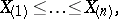
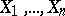 .
.
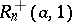 and
and 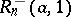 satisfy the same probability law and, if
satisfy the same probability law and, if 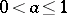 , then
, then


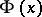 is the distribution function of the standard normal law (cf. Normal distribution) and
is the distribution function of the standard normal law (cf. Normal distribution) and 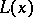 is the Rényi distribution function,
is the Rényi distribution function,
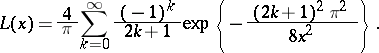
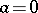 , then
, then
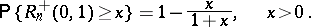
 the following approximate values may be used to calculate the
the following approximate values may be used to calculate the 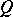 -percent critical values
-percent critical values 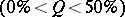 for the statistics
for the statistics 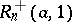 and
and 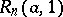 :
:
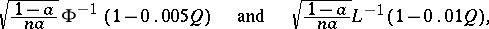
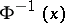 and
and 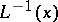 are the inverse functions to
are the inverse functions to 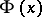 and
and 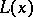 , respectively. This means that if
, respectively. This means that if 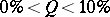 , then
, then 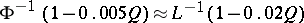 .
.
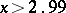 , then it is advisable to use the approximate equation
, then it is advisable to use the approximate equation
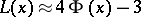
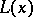 ; its degree of error does not exceed
; its degree of error does not exceed 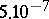 .
.
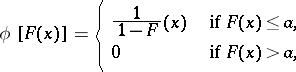
 is any fixed number from the interval
is any fixed number from the interval 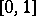 .
.