Fourier integral operator

An integral operator with a generalized kernel that is a rapidly-oscillating function or the integral of such a function. Operators of this type arose when investigating the asymptotic expansions of rapidly-oscillating solutions to partial differential equations (see [1], [2]) and in studying the singularities of the fundamental solutions of hyperbolic equations (see [1], [2], [3]).

The Maslov canonical operator.

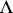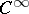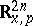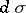Let be an -dimensional Lagrangian manifold of class in the phase space , where , and let be the volume element on 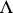. A canonical atlas is a locally finite countable covering of 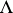by bounded simply-connected domains 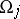(the charts) in each of which one can take as coordinates either the variables or 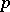or a mixed collection

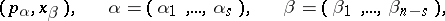not containing dual pairs 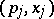. The Maslov canonical operator sends 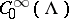into 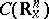. The canonical operators 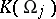are introduced as follows.

1) Let the chart 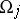be non-degenerate, that is, 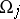is given by an equation 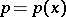and

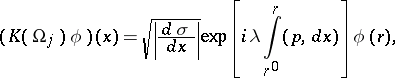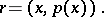Here 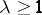is a parameter, 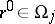is a fixed point, 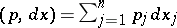, and .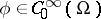

2) Let the local coordinates in the chart 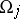be 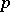, that is, 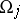is given by an equation 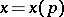, and let

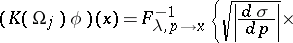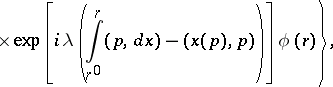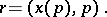Here 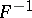is the Fourier 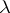-transform

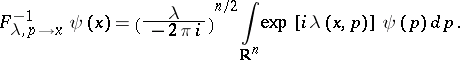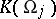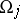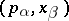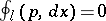is defined analogously in the case when the coordinates in are some collection . Let and let the Maslov index 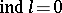for any closed path 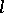lying on 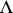. One introduces a partition of unity of class 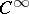on :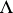

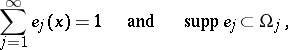and one fixes a point 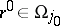. The Maslov canonical operator is defined by

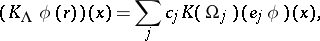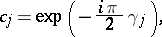and 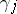is the Maslov index of a chain of charts joining the charts 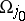and .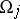

A point 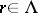is called non-singular if it has a neighbourhood in 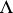given by an equation 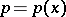. Let the intersection of the charts 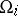and 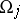be non-empty and connected, let 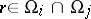be a non-singular point and let 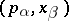, 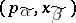be the coordinates in these charts. The number

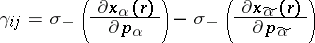is the Maslov index of the pair of charts 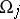and 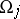, where 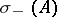is the number of negative eigen values of the matrix 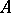. The Maslov index of a chain of charts is defined by additivity. The Maslov index of a path 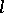is defined analogously. The Maslov index of a path (mod 4) on a Lagrangian manifold is an integer homotopy invariant (see [1], [3]). The Maslov canonical operator is invariant under the choice of the canonical atlas, of local coordinates in the charts and the partition of unity in the following sense: If 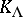, 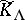are two Maslov canonical operators, then in ,

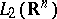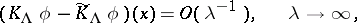for any function .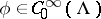

The most important result in the theory of Maslov canonical operators is the commutation formula for the Maslov canonical operator and the 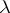-differential (or 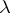-pseudo-differential [3]) operator.

Let 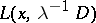be a differential operator with real symbol 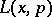of class 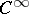(cf. Symbol of an operator) and suppose that 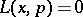on 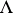. Suppose that 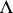and the volume element 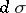are invariant under the Hamiltonian system

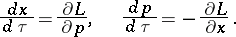Then the following commutation formula is true (here , ):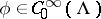

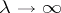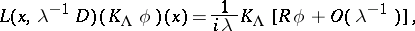(1)

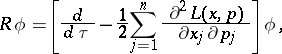where 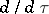is the derivative along the integral curves of the flow of the Hamiltonian system. For the other terms in the expansion (1) and an estimate for the remainder term see [3]. The equation 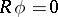is called the transport equation. The commutation formula implies that if 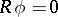, then the function 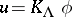is a formal asymptotic solution of the equation .

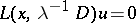The method of the Maslov canonical operator enables one to solve the following problems.

1) The construction of an asymptotic solution to the Cauchy problem with rapidly-oscillating initial data in the large (that is, over any finite time interval) for strictly-hyperbolic systems of partial differential equations, for Dirac and Maxwell systems, for systems in the theory of elasticity, for the Schrödinger equation (see [1], [9]–[6] and also Quasi-classical approximation) and also the construction of solutions to certain mixed problems [4].

2) The construction of asymptotic expansions for the series of eigen values of self-adjoint differential operators associated with Lagrangian manifolds that are invariant under the corresponding Hamiltonian system (see [1], [3]).

3) The construction of asymptotic expansions up to smooth functions for the fundamental solution of a strictly-hyperbolic system of partial differential equations (see [1], [5], [6]).

4) The construction of shortwave asymptotics of the Green function, of the solution to the scattering problem and of the scattering amplitude for the Schrödinger equation, and of the asymptotics for the spectral function (see [5]–[7]).

A new version of the Maslov canonical operator has been developed on Lagrangian manifolds with complex fibres (see [8], [9]).

The Fourier integral operator.

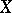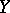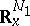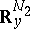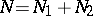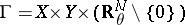Let , be bounded domains in , , , let and let 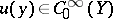. The operator

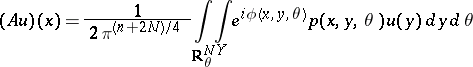(2)

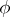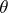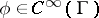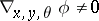is called a Fourier integral operator. Here (the phase function) is real and positively homogeneous of degree 1 in , , and when 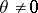. The function 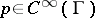(the symbol) has in the simplest case an asymptotic expansion, as ,

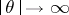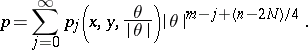The integral (2) converges after corresponding regularization and defines a continuous linear operator 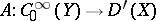. The kernel of 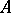is

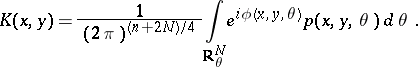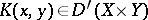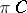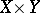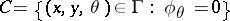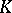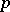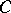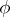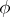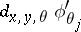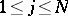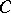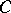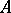The function is infinitely differentiable outside the projection on of the set . The singularities of depend only on the Taylor expansion of the symbol in a neighbourhood of (for a fixed phase ). Let the phase be non-degenerate, that is, let the differentials , , be linearly independent on ; then is a smooth manifold of dimension . 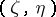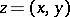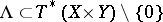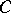To the operator corresponds a smooth, conic (in the variables dual to ) Lagrangian manifold of dimension — it is the image of under the mapping

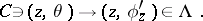(3)

From now on, the operator 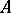is considered on densities 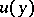of order :

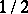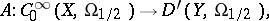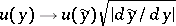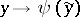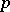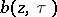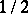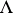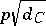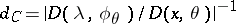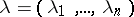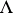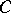that is, under the change of variables . To the symbol corresponds the density of order on that is the image of under the mapping (3), where and are the coordinates on , homogeneous of degree 1 in , carried over to by means of (3). As 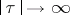, the density 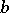has an asymptotic expansion

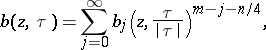the coefficient 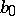is called the principal symbol of the operator .

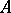Let the operator 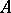be represented in the form (2) but with another non-degenerate phase function 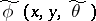, , 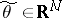and with another symbol 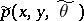. Then for this representation the manifold 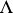remains the same, the quantity 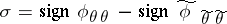is constant and the principal symbol 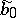is

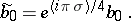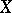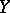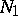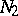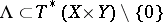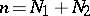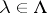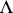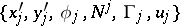The general definition of a Fourier integral operator is as follows. Let , be smooth manifolds of dimensions , and let be a conic smooth Lagrangian manifold of dimension . For any point there is a non-degenerate phase function such that the Lagrangian manifold constructed with respect to it coincides locally with . Let be the set of objects consisting of:

a) local coordinate neighbourhoods 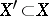, 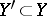with local coordinates , , ;

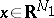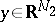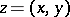b) an integer 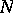and a non-degenerate phase function 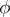defined on 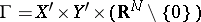such that the mapping

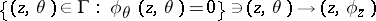is a diffeomorphism onto an open subset 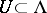. The operator

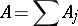is called a Fourier integral operator, where 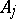has the form (2), 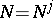, 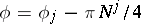and the support of the symbol 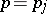lies in 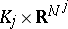, where 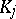is a compact set in 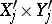. The class of such operators 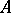is denoted by .

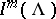Let 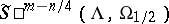be the set of homogeneous densities of order 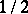that are of degree 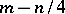with respect to on 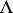. From the principal symbols 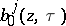of the operators 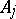one can construct in a natural way the principal symbol 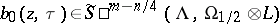of 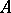such that the mapping

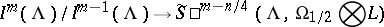is an isomorphism (see [2], [14]).

The most important case for applications of Fourier integral operators to partial differential equations is when the projections 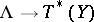are local diffeomorphisms. Then 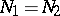, the density 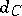is equal to

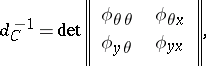and the operator

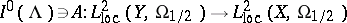is bounded.

Just as for the Maslov canonical operator there are commutation formulas for Fourier integral operators with differential operators, as well as all implications following from these. Locally a Fourier integral operator can be represented as an integral with respect to a parameter over the Maslov canonical operator (see [10]). The Fourier integral operator is applied:

1) to construct parametrices and to study the micro-local structure of the singularities (wave front sets) of solutions to hyperbolic equations, equations of principal type and boundary value problems (see [2], [14]);

2) to investigate the question of the local and global solvability and subellipticity of equations (see [12]); and

3) to obtain asymptotic expansions for the spectral functions of pseudo-differential operators (see [13]).

References

[1]	V.P. Maslov, "Théorie des perturbations et méthodes asymptotiques" , Dunod (1972) (Translated from Russian)
[2]	L. Hörmander, "Fourier integral operators, I" Acta Math. , 127 (1971) pp. 79–183
[3]	V.P. Maslov, M.V. Fedoryuk, "Quasi-classical approximation for the equations of quantum mechanics" , Reidel (1981) (Translated from Russian)
[4]	M.V. Fedoryuk, "Singularities of the kernels of Fourier integral operators and the asymptotic behaviour of the solution of the mixed problem" Russian Math. Surveys , 32 : 6 (1977) pp. 67–120 Uspekhi Mat. Nauk , 32 : 6 (1977) pp. 67–115
[5]	V.V. Kucherenko, "Semi-classical asymptotics of a point source function for a steady-state Schrödinger equation" Teoret. i Mat. Fiz. , 1 (1969) pp. 384–406 (In Russian)
[6]	B.R. Vainberg, "Asymptotic methods in the equations of mathematical physics" , Gordon & Breach (1988) (Translated from Russian)
[7]	B.R. Vainberg, "A complete asymptotic expansion of the spectral function of second order elliptic operators in 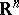" Math. USSR-Sb. , 51 : 1 (1985) pp. 191–206 Mat. Sb. , 123 : 2 (1984) pp. 195–211
[8]	V.V. Kucherenko, "Asymptotic solution of the Cauchy problem for equations with complex characteristics" J. Soviet Math. , 13 : 1 (1980) pp. 24–118 Itogi Nauk. i Tekhn. Sovr. Probl. Mat. , 8 (1977) pp. 41–136
[9]	V.P. Maslov, "Operational methods" , MIR (1976) (Translated from Russian)
[10]	A.S. Mishchenko, B.Yu. Sternin, V.E. Shatalov, "Lagrangian manifolds and the method of the canonical operator" , Moscow (1978) (In Russian)
[11]	J. Leray, "Lagrangian analysis and quantum mechanics" , M.I.T. (1981) (Translated from French)
[12]	Yu.B. Egorov, "Subelliptic operators" Russian Math. Surveys , 30 : 2 (1975) pp. 59–118 Uspekhi Mat. Nauk , 30 : 2 (1975) pp. 57–114
[13]	M.A. Shubin, "Pseudo differential operators and spectral theory" , Springer (1987) (Translated from Russian)
[14]	F. Trèves, "Introduction to pseudodifferential and Fourier integral operators" , 1–2 , Plenum (1980)

Comments

The approach through asymptotic expansions of rapidly-oscillating solutions to partial differential equations is given in [a5], [a6], while [a4] approaches Fourier integral operators from the study of fundamental solutions of hyperbolic equations.

Concerning singularities of the Lagrangian manifold 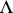see [a5]. The fact that the Maslov index (mod 4) is a homotopy invariant can also be found in [a3]. Concerning (higher-order terms in) (1) see [a4], [a6]. For the use of the Maslov index see [a2], [a6].

For Fourier integral operators in the construction of parametrices, the structure of singularities and the solvability and subellipticity problems for equations see [a4].

The connection with asymptotic expansions can be found in [a7], [a8].

Fourier integral operators with complex phase functions were developed in [a9].

[a10] -[a14] are some (recent) textbooks.

References

[a1]	L.V. Hörmander, "The analysis of linear partial differential operators" , 4. Fourier integral operators , Springer (1985)
[a2]	P.D. Lax, "Asymptotic solutions of oscillatory initial value problems" Duke Math. J. , 24 (1957) pp. 627–646
[a3]	V.I. Arnol'd, "Characteristic class entering in quantization conditions" Funct. Anal. Appl. , 1 (1967) pp. 1–13 Funkts. Anal. i Prilozhen. , 1 (1967) pp. 1–14
[a4]	J.J. Duistermaat, L. Hörmander, "Fourier integral operators II" Acta Math. , 128 (1972) pp. 183–269
[a5]	V.I. Arnol'd, "Integrals of rapidly oscillating functions and singularities of projections of Lagrangian manifolds" Funct. Anal. Appl. , 6 (1972) pp. 222–224 Funkts. Anal. i Prilozhen. , 6 (1972) pp. 61–62
[a6]	J.J. Duistermaat, "Oscillatory integrals, Lagrange immersions and unfoldings of singularities" Comm. Pure Appl. Math. , 27 (1974) pp. 207–281
[a7]	J. Chazarain, "Formules de Poisson pour les variétés riemanniennes" Invent. Math. , 24 (1974) pp. 65–82
[a8]	J.J. Duistermaat, V.W. Guillemin, "The spectrum of positive elliptic operators and periodic bicharacteristics" Invent. Math. , 29 (1975) pp. 39–79
[a9]	A. Melin, J. Sjöstrand, "Fourier integral operators with complex phase functions and parametrix for an interior boundary value problem" Comm. Part. Diff. Equations , 1 (1976) pp. 313–400
[a10]	M.E. Taylor, "Pseudo-differential operators" , Princeton Univ. Press (1981)
[a11]	B.E. Petersen, "Introduction to the Fourier transform and pseudo-differential operators" , Pitman (1983)
[a12]	J. Chazarain, A. Piriou, "Introduction to the theory of partial differential equations" , North-Holland (1982) (Translated from French)
[a13]	J.J. Duistermaat, "Fourier integral operators" , Courant Inst. Math. (1973)
[a14]	J. Dieudonné, "Eléments d'analyse" , 7–8 , Gauthier-Villars (1978)