Inclusion of summation methods
An inclusion of the summability fields (cf. Summability field) corresponding to these methods. Let  and
and  be two summation methods defined on a set
be two summation methods defined on a set  of series (or sequences); let
of series (or sequences); let  and
and 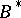 be their summability fields and suppose
be their summability fields and suppose  ; one then says that method
; one then says that method  includes method
includes method  , which is denoted by the symbol
, which is denoted by the symbol  . Methods
. Methods  and
and 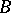 are said to be equipotent, denoted by
are said to be equipotent, denoted by 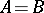 , if each of them includes the other. Equipotent methods have the same summability field. Method
, if each of them includes the other. Equipotent methods have the same summability field. Method  is said to be stronger than method
is said to be stronger than method 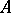 if
if 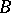 includes
includes 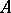 but is not equipotent with it. If the summability field of the method is identical with the set of all convergent series, the method is said to be equipotent with convergence. An inclusion of summation methods is sometimes considered not on the entire set of their definition, but only on some of its subsets.
but is not equipotent with it. If the summability field of the method is identical with the set of all convergent series, the method is said to be equipotent with convergence. An inclusion of summation methods is sometimes considered not on the entire set of their definition, but only on some of its subsets.
For the Cesàro summation methods 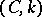 the inclusion
the inclusion 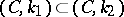 is valid for
is valid for 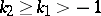 ; the Abel summation method is stronger than all Cesàro methods
; the Abel summation method is stronger than all Cesàro methods  for
for  ; the Riesz summation method
; the Riesz summation method 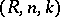 is equipotent with the Cesàro summation method
is equipotent with the Cesàro summation method 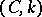 (
( ); the Abel summation method is equipotent with convergence on the set of series whose terms
); the Abel summation method is equipotent with convergence on the set of series whose terms 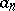 satisfy the condition
satisfy the condition  . In these examples the summation methods are compatible as well (cf. Compatibility of summation methods), even though, in general, an inclusion of summation methods does not rest on the assumption of their being compatible. However, if
. In these examples the summation methods are compatible as well (cf. Compatibility of summation methods), even though, in general, an inclusion of summation methods does not rest on the assumption of their being compatible. However, if 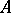 and
and 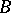 are regular matrix methods (cf. Regular summation methods) and
are regular matrix methods (cf. Regular summation methods) and  on the set of bounded sequences, then
on the set of bounded sequences, then 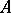 and
and 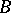 are compatible on this set (the Mazur–Orlicz–Brudno theorem). The compatibility requirement is imposed in the very definition of inclusion in certain textbooks.
are compatible on this set (the Mazur–Orlicz–Brudno theorem). The compatibility requirement is imposed in the very definition of inclusion in certain textbooks.
An inclusion of summation methods defined on a set of series with real terms is said to be complete if the inclusion of their summability fields is preserved after these fields have been completed with series summable to 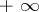 and
and 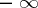 . Thus, the Hölder summation method (cf. Hölder summation methods)
. Thus, the Hölder summation method (cf. Hölder summation methods)  completely includes the Cesàro method
completely includes the Cesàro method 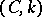 .
.
An inclusion of summation methods for special types of summability (e.g. absolute summability, strong summability, etc.) is defined in a similar manner.
References
| [1] | G.H. Hardy, "Divergent series" , Oxford Univ. Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
| [3] | G.P. Kangro, "Theory of summability of sequences and series" J. Soviet Math. , 5 : 1 (1976) pp. 1–45 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 5–70 |
| [4] | S. Mazur, W. Orlicz, "Sur les méthodes linéaires de sommation" C.R. Acad. Sci. Paris Sér. I Math. , 196 (1933) pp. 32–34 |
| [5] | A.L. Brudno, "Summability of bounded sequences of matrices" Mat. Sb. , 16 (58) : 2 (1945) pp. 191–247 (In Russian) (English abstract) |
| [6] | S.A. Baron, "Introduction to the theory of summability of series" , Tartu (1966) (In Russian) |
Inclusion of summation methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Inclusion_of_summation_methods&oldid=15184