Positive cone

A subset 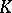of a real vector space 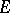satisfying the following conditions:

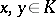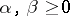1) if and , then ;

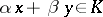2) .

A positive cone defines a pre-order in 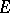by putting 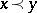if 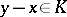. (This pre-order is compatible with the vector space operations.)

Let 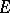be a Banach space. The cone 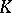is a closed reproducing positive cone if for all 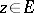there are 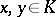such that 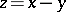. In that case there is a constant independent of such that there always exist 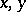such that 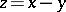with 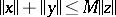. A solid positive cone, i.e. one having interior points, is reproducing.

Let 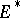be the dual of the Banach space 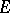. If 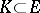is a closed reproducing positive cone, then the set 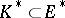of positive functionals (with respect to the positive cone, i.e. those 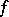such that 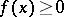for 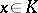) is also a positive cone (this is the so-called conjugate cone). The positive cone can be recovered from 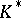, namely:

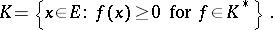If 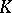is a solid positive cone, then its interior coincides with

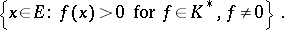A cone in the Banach space is called normal if one can find a 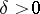so that 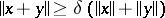for 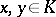. A positive cone is normal if and only if the conjugate cone 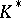is reproducing. If 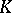is a reproducing cone, then the conjugate cone 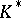is normal.

A cone 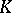is called a lattice cone if each pair of elements 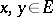has a least upper bound 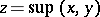, i.e. and for any 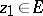it follows from 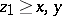that 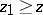. If a positive cone is regular and lattice, then any countable bounded subset has a least upper bound.

References

[1]	M.A. Krasnosel'skii, "Positive solutions of operator equations" , Wolters-Noordhoff (1964) (Translated from Russian)

References

[a1]	H.H. Schaefer, "Banach lattices and positive operators" , Springer (1974)
[a2]	A.C. Zaanen, W. Luxemburg, "Riesz spaces" , I , North-Holland (1983)