Weil cohomology
Cohomology of algebraic varieties with coefficients in a field of characteristic zero, with formal properties required to obtain the Lefschetz formula for the number of fixed points. The necessity for such a theory was pointed out by A. Weil [1], who showed that the rationality of the zeta-function and 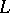 -function of a variety over a finite field follow from the Lefschetz formula, whereas the remaining hypotheses about the zeta-function can naturally be formulated in cohomological terms. Let the variety
-function of a variety over a finite field follow from the Lefschetz formula, whereas the remaining hypotheses about the zeta-function can naturally be formulated in cohomological terms. Let the variety 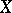 be a projective smooth connected scheme over a fixed algebraically closed field
be a projective smooth connected scheme over a fixed algebraically closed field 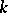 and let
and let 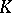 be a field of characteristic zero. Then Weil cohomology with coefficient field
be a field of characteristic zero. Then Weil cohomology with coefficient field 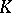 is a contravariant functor
is a contravariant functor 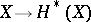 from the category of varieties into the category of finite-dimensional graded anti-commutative
from the category of varieties into the category of finite-dimensional graded anti-commutative 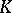 -algebras, which satisfies the following conditions:
-algebras, which satisfies the following conditions:
1) If 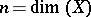 , then
, then  is isomorphic to
is isomorphic to 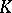 , and the mapping
, and the mapping
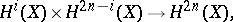 |
defined by the multiplication in  , is non-degenerate for all
, is non-degenerate for all  ;
;
2) 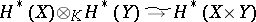 (Künneth formula);
(Künneth formula);
3) Mapping of cycles. There exists a functorial homomorphism 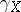 from the group
from the group 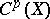 of algebraic cycles in
of algebraic cycles in 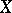 of codimension
of codimension 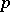 into
into 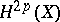 which maps the direct product of cycles to the tensor product and is non-trivial in the sense that, for a point
which maps the direct product of cycles to the tensor product and is non-trivial in the sense that, for a point 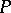 ,
, 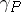 becomes the canonical imbedding of
becomes the canonical imbedding of 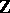 into
into 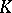 . The number
. The number
 |
is known as the 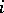 -th Betti number of the variety
-th Betti number of the variety 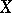 .
.
Examples. If 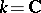 , classical cohomology of complex manifolds with coefficients in
, classical cohomology of complex manifolds with coefficients in 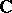 is a Weil cohomology. If
is a Weil cohomology. If 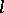 is a prime number distinct from the characteristic of the field
is a prime number distinct from the characteristic of the field 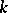 , then étale
, then étale 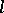 -adic cohomology
-adic cohomology
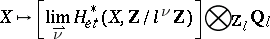 |
is a Weil cohomology with coefficients in the field 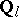 .
.
The Lefschetz formula
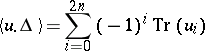 |
is valid for Weil cohomology. In the above formula, 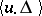 is the intersection index in
is the intersection index in 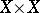 of the graph
of the graph 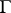 of the morphism
of the morphism 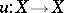 with the diagonal
with the diagonal 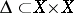 , which may also be interpreted as the number of fixed points of the endomorphism
, which may also be interpreted as the number of fixed points of the endomorphism  , while
, while 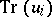 is the trace of the endomorphism
is the trace of the endomorphism 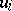 which is induced by
which is induced by  in
in 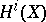 . Moreover, this formula is also valid for correspondences, i.e. elements
. Moreover, this formula is also valid for correspondences, i.e. elements 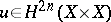 .
.
References
| [1] | A. Weil, "Numbers of solutions of equations in finite fields" Bull. Amer. Math. Soc. , 55 (1949) pp. 497–508 |
| [2] | S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386 |
Comments
References
| [a1] | A. Grothendieck, "The cohomology theory of abstract algebraic varieties" J.A. Todd (ed.) , Proc. Internat. Congress Mathematicians (Edinburgh, 1958) , Cambridge Univ. Press (1960) pp. 103–118 |
| [a2] | A. Grothendieck, I. Bucur, C. Honzel, L. Illusie, J.-P. Jouanolou, J.-P. Serre, "Cohomologie  -adique et fonctions -adique et fonctions  . SGA 5" , Lect. notes in math. , 589 , Springer (1977) . SGA 5" , Lect. notes in math. , 589 , Springer (1977) |
| [a3] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) |
| [a4] | E. Freitag, R. Kiehl, "Étale cohomology and the Weil conjecture" , Springer (1988) |
| [a5] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 272 |
Weil cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_cohomology&oldid=15121