Central product of groups
From Encyclopedia of Mathematics
A group-theoretical construction. A group 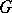 is called a central product of two of its subgroups
is called a central product of two of its subgroups 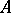 and
and 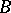 if it is generated by them, if
if it is generated by them, if 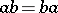 for any two elements
for any two elements 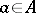 and
and 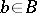 and if the intersection
and if the intersection 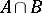 lies in its centre
lies in its centre 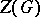 . In particular, for
. In particular, for 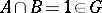 the central product turns out to be the direct product
the central product turns out to be the direct product 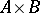 . If
. If 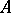 ,
, 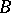 and
and 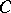 are arbitrary groups such that
are arbitrary groups such that 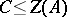 and if
and if 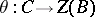 is a monomorphism, then the central product of
is a monomorphism, then the central product of 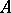 and
and  can be defined without assuming in advance that
can be defined without assuming in advance that 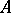 and
and 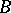 are subgroups of a certain group
are subgroups of a certain group 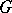 .
.
References
| [1] | D. Gorenstein, "Finite groups" , Harper & Row (1968) |
How to Cite This Entry:
Central product of groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Central_product_of_groups&oldid=15113
Central product of groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Central_product_of_groups&oldid=15113
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article