Representation of matrices, problem of

problem of presentation of matrices

The problem of whether one can exhibit a unified general method (an algorithm) that would give, in a finite number of steps, an answer to the question whether a matrix 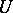can be represented by matrices 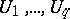using multiplication, for any system 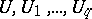of matrices over integers. The case in which 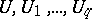are square matrices of the same order is of most interest. This formulation of the problem of presentation of matrices is called general. By fixing the matrices 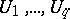and leaving the matrix 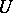variable one obtains the partial problem of presentation of matrices. An algorithm solving the general formulation also solves all partial problems, since for establishing the unsolvability of the general formulation it is sufficient to exhibit at least one unsolvable partial problem.

The problem of presentation of matrices is one of the first algorithmic problems (cf. Algorithmic problem) of algebraic character whose unsolvability was established. It was originally proved by A.A. Markov (cf. [1], [2]) that for 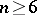one can construct a system, consisting of 91 matrices of order , such that the corresponding partial problem is unsolvable, i.e. there is no algorithm (in an exact sense of this word) recognizing for an arbitrary matrix of order whether it can be presented by matrices of this system. Subsequently (cf. [3]) the number of matrices in the system was reduced to 23 and it was proved that, with an appropriate complication in the construction of the system, the condition 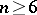could be weakened to 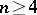. For any 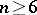one can construct a concrete system, consisting of 12 matrices of order , with unsolvable partial problem (cf. [4]). By appropriately fixing 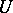and varying 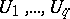the unsolvability of the general formulation has been proved for 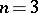(cf. [5]).

References

[1]	A.A. Markov, "On an unsolvable problem concerning matrices" Dokl. Akad. Nauk SSSR , 78 : 6 (1951) pp. 1089–1092 (In Russian)
[2]	A.A. Markov, "Theory of algorithms" , Israel Program Sci. Transl. (1961) (Translated from Russian) (Also: Trudy Mat. Inst. Steklov. 42 (1954))
[3]	A.A. Markov, "On the problem of presenting matrices" Z. Math. Logik und Grundl. Math. , 4 (1958) pp. 157–168 (In Russian) (German abstract)
[4]	N.M. Nagornyi, , 6-th All-Union Congress on Math. Logic , Tbilisi (1982) pp. 124 (In Russian)
[5]	M.S. Paterson, "Unsolvability in 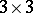matrices" Stud. in Appl. Math. , 49 : 1 (1970) pp. 105–107