Divergence

of a vector field at a point

The scalar field

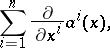where are the components of the vector field .

The divergence is denoted by or by the inner product of the Hamilton operator and the vector .

If the vector field is the field of velocities of a stationary flow of a non-compressible liquid, 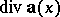coincides with the intensity of the source (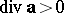) or the sink (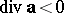) at the point .

The integral

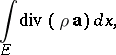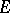where is the density of the liquid computed for the -dimensional domain , is equal to the amount of the liquid "issuing" from in unit time. This amount (cf. Ostrogradski formula) coincides with the magnitude

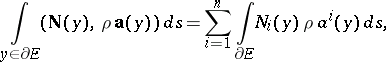where is the unit exterior normal vector to , and is the area element of . The divergence is the derivative with respect to the rate of the flow across the closed surface:

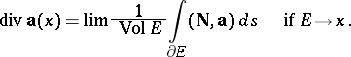Thus, the divergence is invariant with respect to the choice of the coordinate system.

In curvilinear coordinates , , ,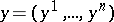

(*)

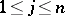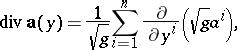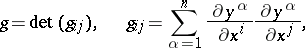where

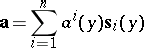and is the unit tangent vector to the -th coordinate line at the point :

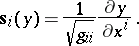The divergence of a tensor field

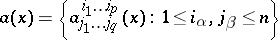of type 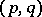defined in a domain of an -dimensional manifold with an affine connection, is defined with the aid of the corresponding absolute (covariant) derivatives of the components of 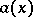, with subsequent convolution (contraction), and is a tensor of type with components

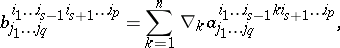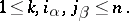In tensor analysis and differential geometry a differential operator operating on the space of differential forms and connected with the operator of exterior differentiation is also called a divergence.

References

[1]	N.E. Kochin, "Vector calculus and fundamentals of tensor calculus" , Moscow (1965) (In Russian)
[2]	P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)

Comments

The Hamilton operator is usually called nabla operator, after the symbol for it, . Ostrogradski's formula is better known as the Gauss–Ostrogradski or Gauss formula.

For other vector differentiation operators see Curl; Gradient. For relations between these see also Vector analysis.

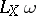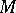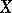Let be an -dimensional manifold and a volume element on . The Lie derivative is then also a differential -form and so for some function on . This function is the divergence of with respect to the volume element 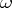. If 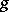is a Riemannian metric on , then the divergence of as defined by (*) above is the divergence of with respect to the volume element 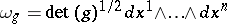defined by . For any function , is an -form, so is defined — the integral of a function 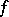with respect to a volume element 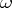. If is compact, then Green's theorem says that

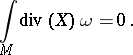Still another notation for the divergence of an -tuple of functions of (or of a vector field) is .

References

[a1]	D.E. Bourne, P.C. Kendall, "Vector analysis and Cartesian tensors" , Nelson & Sons , Sunbury-on-Thames (1977)