Mann theorem
A theorem giving an estimate of the density of the sum of two sequences (cf. Density of a sequence). Let 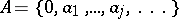 be an increasing sequence of integers and let
be an increasing sequence of integers and let
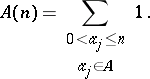 |
The density of the sequence 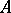 is the quantity
is the quantity
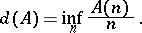 |
The arithmetic sum of two sequences 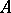 and
and 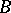 is the sequence
is the sequence 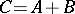 consisting of all possible sums
consisting of all possible sums 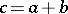 , where
, where 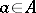 and
and 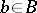 . Mann's theorem asserts that
. Mann's theorem asserts that
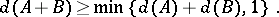 |
Mann's theorem implies that if 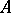 is a sequence of positive density less than 1 and
is a sequence of positive density less than 1 and 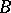 is another sequence of positive density, then on addition of
is another sequence of positive density, then on addition of 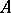 and
and 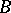 the density is increased. Another important consequence of Mann's theorem is: Each sequence of positive density is a basis for the sequence of natural numbers. Mann's theorem essentially strengthens a similar theorem of Shnirel'man (cf. Shnirel'man method). It was proved by H.B. Mann [1].
the density is increased. Another important consequence of Mann's theorem is: Each sequence of positive density is a basis for the sequence of natural numbers. Mann's theorem essentially strengthens a similar theorem of Shnirel'man (cf. Shnirel'man method). It was proved by H.B. Mann [1].
References
| [1] | H.B. Mann, "A proof of the fundamental theorem on the density of sums of sets of positive integers" Ann. of Math. , 43 (1942) pp. 523–527 |
| [2] | H.H. Ostmann, "Additive Zahlentheorie" , Springer (1956) |
| [3] | A.O. Gel'fond, Yu.V. Linnik, "Elementary methods in the analytic theory of numbers" , M.I.T. (1966) (Translated from Russian) |
Mann theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mann_theorem&oldid=15059