Dirichlet theorem

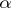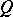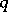Dirichlet's theorem in the theory of Diophantine approximations: For any real number and any natural number there exist integers and which satisfy the condition

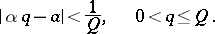With the aid of the Dirichlet box principle a more general theorem can be demonstrated: For any real numbers and any natural number 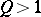there exist integers and 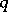such that

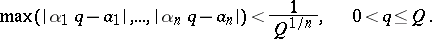References

[1]	J.W.S. Cassels, "An introduction to diophantine approximation" , Cambridge Univ. Press (1957)

V.I. Bernik

Dirichlet's unit theorem. A theorem describing the structure of the multiplicative group of units of an algebraic number field; obtained by P.G.L. Dirichlet [1].

Each algebraic number field 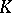of degree over the field of rational number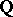s has different isomorphisms into the field of complex numbers . If under the isomorphism 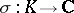the image of the field is contained in the field of real numbers, this isomorphism is said to be real; otherwise it is said to be complex. Each complex isomorphism has a complex conjugate isomorphism 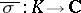, defined by the equation 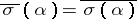, 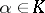. In this way the number may be represented as 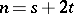, where is the number of real and 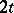is the number of complex isomorphisms of 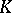into .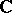

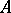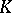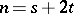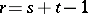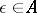Dirichlet's theorem: In an arbitrary order of an algebraic number field of degree there exist units such that any unit is uniquely representable as a product

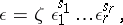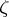where are integers and is some root of unity contained in . The units , the existence of which is established by Dirichlet's theorem, are said to be the basic units of the order 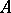. In particular, the basic units of the maximal order 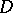of the field 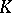, i.e. the ring of integers of 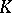, are usually called basic units of the algebraic number field .

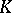References

[1]	P.G.L. Dirichlet, "Werke" , 1 , Springer (1889)
[2]	Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966)

S.A. Stepanov

Dirichlet's theorem on prime numbers in an arithmetical progression: Each arithmetical progression whose first term and difference are relatively prime contains an infinite number of prime numbers. It was in fact proved by P.G.L. Dirichlet [1] that for any given relatively prime numbers ,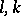

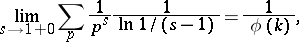where the summation is effected over all prime numbers 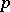subject to the condition 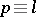(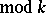) and 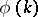is Euler's function. This relation may be interpreted as the law of uniform distribution of prime numbers over the residue classes 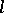(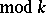), since

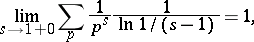where the summation is extended over all prime numbers.

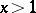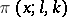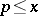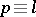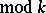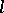Let be an integer and let be the amount of prime numbers subject to the condition (), where and and 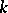are relatively prime. Then

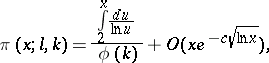where the estimate of the remainder is uniform in for any given 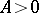, and 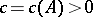is a magnitude which depends only on 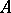(non-effectively). This is the modern form of Dirichlet's theorem, which immediately indicates the nature of the distribution of the prime numbers 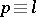(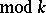) in the series of natural numbers. It is believed (the extended Riemann hypothesis) that, for given relatively prime 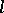and 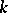and any integer ,

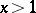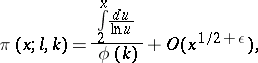where 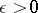is arbitrary, while 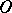is a magnitude depending on 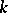and .

References

[1]	P.G.L. Dirichlet, "Vorlesungen über Zahlentheorie" , Vieweg (1894)
[2]	K. Prachar, "Primzahlverteilung" , Springer (1957)
[3]	A.A. Karatsuba, "Fundamentals of analytic number theory" , Moscow (1975) (In Russian)

V.G. Sprindzhuk

Dirichlet's theorem on Fourier series: If a 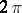-periodic function 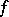is piecewise monotone on the segment 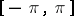and has at most finitely many discontinuity points on it, i.e. if the so-called Dirichlet conditions are satisfied, then its trigonometric Fourier series converges to at each continuity point and to 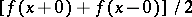at each discontinuity point. First demonstrated by P.G.L. Dirichlet [1]. Dirichlet's theorem was generalized by C. Jordan [3] to functions of bounded variation.

References

[1]	P.G.L. Dirichlet, "Sur la convergence des series trigonométriques qui servent à représenter une fonction arbitraire entre des limites donnés" J. Math. , 4 (1829) pp. 157–169
[2]	P.G.L. Dirichlet, "Werke" , 1 , Springer (1889)
[3]	C. Jordan, C.R. Acad. Sci. , 92 (1881) pp. 228–230
[4]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)
[5]	A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988)