Affine variety

affine algebraic variety

A generalization of the concept of an affine algebraic set. An affine variety is a reduced affine scheme of finite type over a field , i.e. 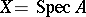, where 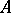is a commutative 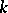-algebra of finite type without nilpotent elements. The affine variety 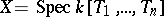, where is the ring of polynomials over 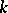, is called affine space over 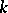and is denoted by 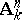. An affine scheme is an affine variety if and only if it is isomorphic to a reduced closed subscheme of an affine space. Each system of generators of a 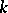-algebra 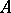defines a surjective homomorphism 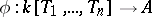, defined by the formula 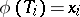. Let 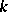be the algebraic closure of 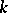. The subset of the set 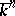consisting of the common zeros of all the polynomials of the ideal 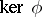is an affine algebraic set over 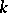. The coordinate ring of such an affine algebraic set is isomorphic to the ring 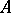. Each affine algebraic set over 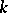in turn defines an algebraic variety 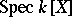, where 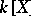is the coordinate ring of 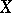. The set of points of an affine variety is in a one-to-one correspondence with the irreducible subvarieties of the corresponding affine algebraic set.

To each affine variety 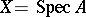a functor on the category of 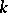-algebras is assigned. It is defined by the correspondence:

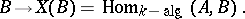If 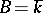(respectively, if 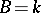), the elements of the set 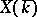(respectively, 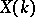) are called geometric (respectively, rational) points of 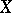. The set 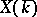is in a bijective correspondence with the set of maximal ideals 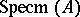of the ring 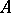, and with the set of points of an algebraic set 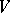whose coordinate ring is isomorphic to 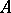. The spectral topology in the space 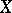induces on the everywhere-dense subset 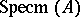a topology which corresponds to the Zariski topology on .

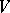Comments

Frequently the name "varietyvariety" means a reduced and irreducible scheme of finite type over an algebraically closed field.

References

[a1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)