Group of covering transformations

of a regular covering

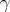The group of those homeomorphisms of the space 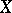onto itself such that . ( and are understood to be connected, locally path-connected, Hausdorff spaces.)

The group of covering transformations of the covering of the circle by the real line given by is thus the group of translations , .

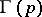is a discrete group of transformations of 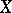acting freely (that is, 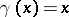for some implies 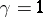), and 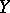is naturally isomorphic to the quotient space . The group is isomorphic to the quotient group of the fundamental group 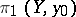, where 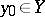, by the image of the group 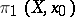, where , under the homomorphism induced by the mapping . In particular, if is the universal covering, then is isomorphic to the fundamental group of .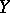

References

[1]	S.-T. Hu, "Homotopy theory" , Acad. Press (1959)

Comments

See also Covering; Universal covering.

References

[a1]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. 2