Subobject
of an object in a category
A concept analogous to the concept of a substructure of a mathematical structure. Let 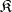 be any category and let
be any category and let 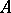 be a fixed object in
be a fixed object in 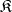 . In the class of all monomorphisms of
. In the class of all monomorphisms of 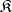 with codomain (target)
with codomain (target) 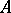 , one may define a pre-order relation (the relation of divisibility from the right):
, one may define a pre-order relation (the relation of divisibility from the right): 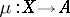 precedes
precedes  , or
, or 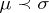 , if
, if  for some
for some 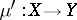 . In fact, the morphism
. In fact, the morphism 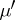 is uniquely determined because
is uniquely determined because 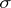 is a monomorphism. The pre-order relation induces an equivalence relation between the monomorphisms with codomain
is a monomorphism. The pre-order relation induces an equivalence relation between the monomorphisms with codomain 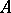 : The monomorphisms
: The monomorphisms 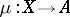 and
and 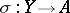 are equivalent if and only if
are equivalent if and only if 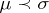 and
and 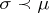 . An equivalence class of monomorphisms is called a subobject of the object
. An equivalence class of monomorphisms is called a subobject of the object 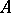 . A subobject with representative
. A subobject with representative 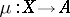 is sometimes denoted by
is sometimes denoted by 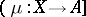 or by
or by 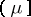 . It is also possible to use Hilbert's
. It is also possible to use Hilbert's  -symbol to select representatives of subobjects of
-symbol to select representatives of subobjects of 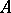 and consider these representatives as subobjects. In the categories of sets, groups, Abelian groups, and vector spaces, a subobject of any object is defined by the imbedding of a subset (subgroup, subspace) in the ambient set (group, space). However, in the category of topological spaces, the concept of a subobject is wider than that of a subset with the induced topology.
and consider these representatives as subobjects. In the categories of sets, groups, Abelian groups, and vector spaces, a subobject of any object is defined by the imbedding of a subset (subgroup, subspace) in the ambient set (group, space). However, in the category of topological spaces, the concept of a subobject is wider than that of a subset with the induced topology.
The pre-order relation between the monomorphisms with codomain 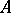 induces a partial order relation between the subobjects of
induces a partial order relation between the subobjects of 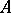 :
: 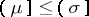 if
if 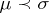 . This relation is analogous to the inclusion relation for subsets of a given set.
. This relation is analogous to the inclusion relation for subsets of a given set.
If the monomorphism 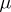 is regular (cf. Normal monomorphism), then any monomorphism equivalent to it is also regular. One can therefore speak of the regular subobjects of any object
is regular (cf. Normal monomorphism), then any monomorphism equivalent to it is also regular. One can therefore speak of the regular subobjects of any object 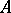 . In particular, the subobject represented by
. In particular, the subobject represented by  is regular. In categories with zero morphisms one similarly introduces normal subobjects. If
is regular. In categories with zero morphisms one similarly introduces normal subobjects. If 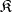 possesses a bicategory structure
possesses a bicategory structure 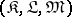 , then a subobject
, then a subobject 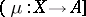 of an object
of an object 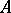 is called admissible (with respect to this bicategory structure) if
is called admissible (with respect to this bicategory structure) if 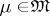 .
.
Comments
The notation  used in this article (and elsewhere in this Encyclopaedia) is not standard. Most authors do not bother to distinguish notationally between a subobject and a monomorphism which represents it.
used in this article (and elsewhere in this Encyclopaedia) is not standard. Most authors do not bother to distinguish notationally between a subobject and a monomorphism which represents it.
For references see Category.
Subobject. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subobject&oldid=15026