Pro-p group

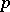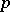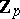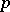A profinite group that is a projective limit of finite -groups (cf. -group). E.g. the additive group of the ring of -adic integers is a pro-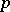-group. In Galois theory pro-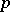-groups appear as Galois groups of 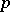-extensions of fields.

Let 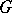be a pro-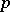-group. A system of generators of 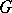is a subset 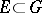with the properties: 1) 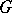is the smallest closed subgroup of 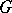generated by ; and 2) any neighbourhood of the identity of 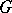contains almost-all (i.e. all except a finite number of) elements of .

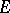Let be an index set and let 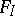be the abstract free group with system of generators 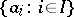. The projective limit 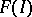of the system of groups 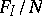, where 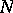is a normal subgroup of 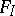such that the index of 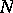in 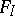is a power of a number 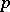, while almost-all elements 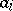, , 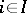lie in 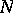, is a pro--group, called the free pro-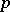-group with system of generators 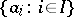. Every closed subgroup of a free pro-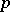-group is itself a free pro-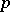-group. Any pro-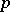-group 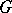is a quotient group of a free pro-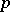-group, i.e. there is an exact sequence of homomorphisms of pro-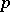-groups,

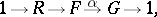where 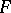is a suitable free pro-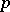-group. (This sequence is called a presentation of 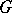by means of 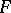.) A subset 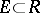is called a system of relations o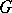f if 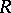is the smallest closed normal subgroup in 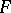containing 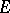and if every open normal subgroup in contains almost-all elements of 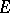. The cardinalities of a minimal (with respect to inclusion) set of generators and a minimal system of relations of a corresponding presentation of a pro-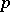-group 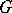have a cohomological interpretation: The first cardinality is the dimension over 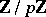of the space 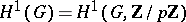, while the second is the dimension over 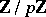of the space . Here 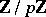is regarded as a discrete 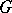-module with a trivial -action. If 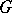is a finite 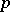-group, then

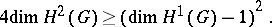This result implies a negative solution to the classical class field tower problem (cf. Tower of fields) [4].

References

[1]	J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964)
[2]	H. Koch, "Galoissche Theorie der -Erweiterungen" , Deutsch. Verlag Wissenschaft. (1970)
[3]	J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1967)
[4]	E.S. Golod, I.R. Shafarevich, "On the class field tower" Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 261–272 (In Russian)