Hit-or-miss topology
This scheme for introducing a topology into a collection of sets (cf. [a1], [a5], [a9]) can be described conveniently by the "hit or miss" metaphor. Given a topological space 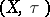 and a collection
and a collection 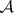 of sets in
of sets in 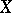 , one introduces a topological structure (topology)
, one introduces a topological structure (topology) 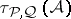 on
on 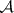 depending on families
depending on families 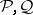 of sets in
of sets in 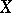 , where
, where 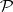 is closed under finite unions, by taking as an open base for
is closed under finite unions, by taking as an open base for 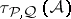 the family of sets of the form
the family of sets of the form
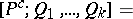 |
 |
The basic open set 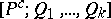 collects those sets in
collects those sets in 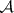 that "miss"
that "miss" 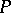 and "hit" every
and "hit" every 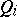 .
.
Important realizations of this scheme are:
1) the exponential topology 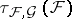 (cf. [a1], [a5], [a9]);
(cf. [a1], [a5], [a9]);
2) the hit-or-miss topology 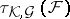 (cf. [a4]);
(cf. [a4]);
3) the myope topology 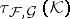 (cf. [a4]). Here,
(cf. [a4]). Here, 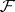 is the collection of all closed sets in
is the collection of all closed sets in 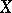 ,
,  is the collection of all open sets in
is the collection of all open sets in 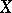 , and
, and 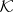 is the collection of all compact sets in
is the collection of all compact sets in 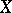 .
.
The hit-or-miss topology is an important tool in mathematical morphology (cf. [a4], [a7]) in Euclidean spaces, hence one most often considers locally compact metric spaces 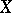 (cf. Locally compact space; Metric space). The topological space
(cf. Locally compact space; Metric space). The topological space 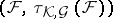 is a compact metric space (cf. [a4]); the topology of this space can be described (cf. [a4]) in terms of convergent sequences: A sequence
is a compact metric space (cf. [a4]); the topology of this space can be described (cf. [a4]) in terms of convergent sequences: A sequence 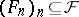 converges in
converges in 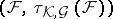 to a set
to a set 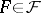 if and only if
if and only if 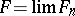 (meaning
(meaning  , where
, where 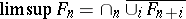 and
and 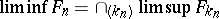 ; see [a3]).
; see [a3]).
The relations of the hit-or-miss topology 2) to the exponential topology 1) and myope topology 3) can be briefly summarized as follows. In general, the exponential topology is finer than the hit-or-miss topology 2) and the myope topology is finer than the restriction 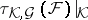 of the hit-or-miss topology to the collection
of the hit-or-miss topology to the collection 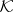 ; the myope topology and the topology
; the myope topology and the topology 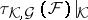 coincide on any subspace
coincide on any subspace  that is compact in the myope topology (compactness of
that is compact in the myope topology (compactness of 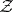 means that
means that 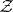 is closed in the hit-or-miss topology and there exists a compact set
is closed in the hit-or-miss topology and there exists a compact set 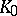 such that
such that 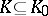 for any
for any 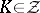 ; cf. [a4]).
; cf. [a4]).
The Hausdorff metric  on the collection
on the collection 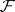 is given by (cf. [a2], [a3]):
is given by (cf. [a2], [a3]):
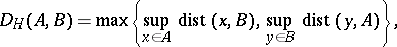 |
where  (
( a bounded metric on
a bounded metric on 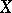 ).
).
The topology 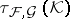 is metrizable (cf. Metrizable space) by
is metrizable (cf. Metrizable space) by 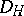 restricted to
restricted to 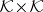 (cf. [a3]); hence the hit-or-miss topology on any subspace
(cf. [a3]); hence the hit-or-miss topology on any subspace 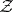 that is compact in the myope topology is metrizable by the metric
that is compact in the myope topology is metrizable by the metric  .
.
A mapping  from a metric space
from a metric space 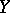 into
into 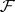 is upper semi-continuous (cf. also Semi-continuous mapping) if
is upper semi-continuous (cf. also Semi-continuous mapping) if 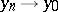 implies
implies
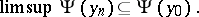 |
An illustration is provided by the basic mappings of mathematical morphology in a Euclidean space 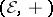 (cf. [a4], [a7]): the opening
(cf. [a4], [a7]): the opening  and the closing
and the closing 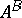 (cf. also Mathematical morphology). Both mappings are upper semi-continuous in the hit-or-miss topology (cf. [a4]). The property of upper semi-continuity implies stability of either of these mappings in the morphological sense (cf. [a7]).
(cf. also Mathematical morphology). Both mappings are upper semi-continuous in the hit-or-miss topology (cf. [a4]). The property of upper semi-continuity implies stability of either of these mappings in the morphological sense (cf. [a7]).
A ramification of the hit-or-miss topology was introduced into collections of rough sets generated from information systems (cf. [a6]) to yield a counterpart of mathematical morphology on abstract data sets (see also [a8]).
References
| [a1] | G. Choquet, "Convergences" Ann. Univ. Grenoble , 23 (1948) pp. 55–112 |
| [a2] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) |
| [a3] | K. Kuratowski, "Topology" , I–II , Acad. Press & PWN (1966–1968) |
| [a4] | G. Matheron, "Random sets and integral geometry" , Wiley (1975) |
| [a5] | E. Michael, "Topologies on spaces of subsets" Trans. Amer. Math. Soc. , 71 (1951) pp. 152–183 |
| [a6] | L. Polkowski, "Mathematical morphology of rough sets" Bull. Polish Acad. Math. , 41 (1993) pp. 241–273 |
| [a7] | J. Serra, "Image analysis and mathematical morphology" , Acad. Press (1982) |
| [a8] | A. Skowron, L. Polkowski, "Analytical morphology" Fundam. Inform. , 26–27 (1996) pp. 255–271 |
| [a9] | L. Vietoris, "Stetige Mengen" Monatsh. Math. und Phys. , 31 (1921) pp. 173–204 |
Hit-or-miss topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hit-or-miss_topology&oldid=14982