Principal fundamental solution

A fundamental solution , defined throughout the space , of a second-order elliptic equation

(*)

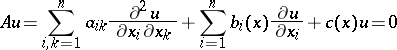that satisfies the conditions

for certain positive constants and if .

If the coefficients , and 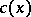satisfy a Hölder condition on 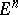and if the inequality is satisfied for some , then a principal fundamental solution exists. If the coefficients of the operator 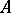are defined in a certain bounded domain with smooth boundary, then they can be extended to the entire space 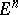so that a principal fundamental solution will exist for the extended operator.

References

[1]	C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian)