Symmetry on a set

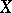
A non-negative real-valued function 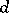defined on the set of all pairs of elements of 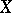and satisfying the following axioms:

1) if and only if ;

2) for any .

In contrast to a metric and a pseudo-metric, a symmetry need not satisfy the triangle axiom. Relative to a symmetry on a set 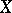there is a topology defined on 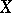: A set 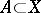is closed (relative to 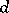) if and only if 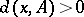for each 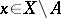. Here

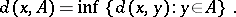The closure of a set 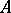in this topological space contains the set of all 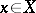for which 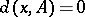but need not be exhausted by this set. Correspondingly, the -ball around a point of 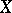may have an empty interior. A topological space is called symmetrizable if its topology is generated by the above rule from some symmetry. The class of symmetrizable spaces is much wider than the class of metrizable spaces (cf. Metrizable space): A symmetrizable space need not be paracompact, normal or Hausdorff. In addition, a symmetrizable space need not satisfy the first axiom of countability.

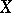However, each symmetrizable space is sequential, that is, its topology is determined by convergent sequences by the rule: A set is closed if and only if the limit of each sequence of points of that converges in belongs to 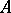. For compact Hausdorff spaces symmetrizability is equivalent to metrizability.

References

[1]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)
[2]	S.I. Nedev, "-metrizable spaces" Trans. Moscow Math. Soc. , 24 (1971) pp. 213–247 Trudy Moskov. Mat. Obshch. , 24 (1971) pp. 201–236