Fano variety
A smooth complete irreducible algebraic variety 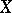 over a field
over a field 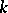 whose anti-canonical sheaf
whose anti-canonical sheaf 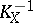 is ample (cf. Ample sheaf). The basic research into such varieties was done by G. Fano ([1], [2]).
is ample (cf. Ample sheaf). The basic research into such varieties was done by G. Fano ([1], [2]).
A Fano variety of dimension 2 is called a del Pezzo surface and is a rational surface. The multi-dimensional analogues of del Pezzo surfaces — Fano varieties of dimension 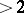 — are not all rational varieties, for example the general cubic in the projective space
— are not all rational varieties, for example the general cubic in the projective space 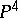 . It is not known (1984) whether all Fano varieties are unirational.
. It is not known (1984) whether all Fano varieties are unirational.
Three-dimensional Fano varieties have been thoroughly investigated (see [3], ). Only isolated particular results are known about Fano varieties of dimension greater than 3.
The Picard group 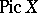 of a three-dimensional Fano variety is finitely generated and torsion-free. In case the ground field
of a three-dimensional Fano variety is finitely generated and torsion-free. In case the ground field 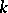 is
is 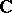 , the rank of
, the rank of 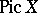 , which is equal to the second Betti number
, which is equal to the second Betti number 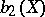 , does not exceed 10 (see [4]). If
, does not exceed 10 (see [4]). If 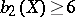 , then the Fano variety is isomorphic to
, then the Fano variety is isomorphic to 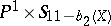 , where
, where 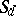 is the del Pezzo surface of order
is the del Pezzo surface of order 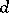 . A Fano variety
. A Fano variety 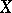 is called primitive if there is no monoidal transformation
is called primitive if there is no monoidal transformation 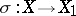 to a smooth variety
to a smooth variety 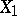 with centre at a non-singular irreducible curve. If
with centre at a non-singular irreducible curve. If 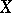 is a primitive Fano variety, then
is a primitive Fano variety, then 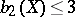 . If
. If 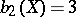 , then
, then 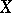 is a conic fibre space over
is a conic fibre space over 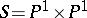 , in other words, then there is a morphism
, in other words, then there is a morphism 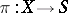 each fibre of which is isomorphic to a conic, that is, an algebraic scheme given by a homogeneous equation of degree 2 in
each fibre of which is isomorphic to a conic, that is, an algebraic scheme given by a homogeneous equation of degree 2 in 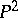 . A Fano variety
. A Fano variety 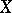 with
with 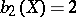 is a conic fibre space over the projective plane
is a conic fibre space over the projective plane 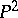 (see [3]). In the case
(see [3]). In the case 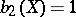 there are 18 types of Fano varieties, which have been classified (see [6]).
there are 18 types of Fano varieties, which have been classified (see [6]).
For three-dimensional Fano varieties 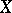 the self-intersection index of the anti-canonical divisor
the self-intersection index of the anti-canonical divisor 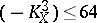 . The largest integer
. The largest integer 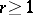 such that
such that 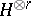 is isomorphic to
is isomorphic to 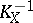 for some divisor
for some divisor 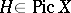 is called the index of the Fano variety. The index of a three-dimensional Fano variety can take the values 1, 2, 3, or 4. A Fano variety of index 4 is isomorphic to the projective space
is called the index of the Fano variety. The index of a three-dimensional Fano variety can take the values 1, 2, 3, or 4. A Fano variety of index 4 is isomorphic to the projective space  , and a Fano variety of index 3 is isomorphic to a smooth quadric
, and a Fano variety of index 3 is isomorphic to a smooth quadric 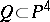 . If
. If 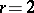 , then the self-intersection index
, then the self-intersection index 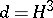 can take the values
can take the values 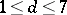 , with each of them being realized for some Fano variety. For a Fano variety of index 1 the mapping
, with each of them being realized for some Fano variety. For a Fano variety of index 1 the mapping 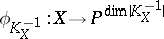 defined by the linear system
defined by the linear system 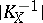 has degree
has degree 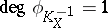 or 2. The Fano varieties of index 1 for which
or 2. The Fano varieties of index 1 for which 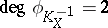 have been classified. If
have been classified. If 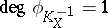 , then
, then 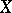 can be realized as a subvariety
can be realized as a subvariety 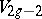 of degree
of degree 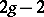 in the projective space
in the projective space 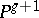 . The number
. The number 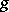 is called the genus of the Fano variety
is called the genus of the Fano variety 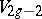 and is the same as the genus of the canonical curve — the section of
and is the same as the genus of the canonical curve — the section of 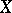 under the anti-canonical imbedding into
under the anti-canonical imbedding into 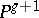 . The Fano varieties
. The Fano varieties 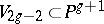 the class of a hyperplane section of which is the same as the anti-canonical class and generates
the class of a hyperplane section of which is the same as the anti-canonical class and generates 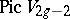 have been classified (see [4], ).
have been classified (see [4], ).
References
| [1] | G. Fano, "Sulle varietà algebriche a tre dimensioni aventi tutti i generi nulu" , Proc. Internat. Congress Mathematicians (Bologna) , 4 , Zanichelli (1934) pp. 115–119 |
| [2] | G. Fano, "Si alcune varietà algebriche a tre dimensioni razionali, e aventi curve-sezioni canoniche" Comment. Math. Helv. , 14 (1942) pp. 202–211 |
| [3] | S. Mori, S. Mukai, "Classification of Fano 3-folds with 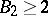 " Manuscripta Math. , 36 : 2 (1981) pp. 147–162 " Manuscripta Math. , 36 : 2 (1981) pp. 147–162 |
| [4] | L. Roth, "Sulle 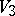 algebriche su cui l'aggiunzione si estingue" Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat. , 9 (1950) pp. 246–250 algebriche su cui l'aggiunzione si estingue" Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Nat. , 9 (1950) pp. 246–250 |
| [5a] | V.A. Iskovskikh, "Fano 3-folds. I" Math. USSR. Izv. , 11 : 3 (1977) pp. 485–527 Izv. Akad. Nauk SSSR Ser. Mat. , 41 : 3 (1977) pp. 516–562 |
| [5b] | V.A. Iskovskikh, "Fano 3-folds. II" Math. USSR. Izv. , 12 : 3 (1978) pp. 469–506 Izv. Akad. Nauk SSSR Ser. Mat. , 42 : 3 (1978) pp. 506–549 |
| [6] | V.A. Iskovskikh, "Anticanonical models of three-dimensional algebraic varieties" J. Soviet Math. , 13 : 6 (1980) pp. 745–850 Itogi Nauk. i Tekhn. Sovr. Probl. Mat. , 12 (1979) pp. 59–157 |
Fano variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fano_variety&oldid=14961