Submersion

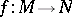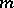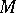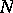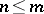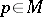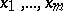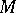A mapping from an -dimensional manifold into an -dimensional manifold , , under which for any point it is possible to introduce local coordinates on near and on near 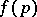such that 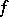is locally represented in terms of these coordinates by

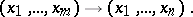If 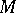and 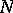possess the structure of a piecewise-linear, -analytic or -differentiable (of class 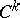) manifold and the local coordinates can be chosen piecewise-linear, -analytic or -differentiable (of class 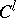, 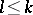), then the submersion is said to be piecewise-linear, -analytic or -differentiable (of class 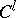). A submersion can also be defined for a manifold with boundary (in topological problems it is advisable to impose an extra condition on the behaviour of the mapping close to the boundary, see [1]) and in the infinite-dimensional case (see [2]). The concept of a submersion in an informal sense is the dual of the concept of an immersion (cf. also Immersion of a manifold), and their theories are analogous.

References

[1]	V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometrical chapters" , Springer (1984) (Translated from Russian)
[2]	S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III

Comments

Submersions are classified by the induced mapping 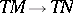of tangent bundles, when 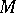is an open manifold. See [a1].

References

[a1]	A. Phillips, "Submersions of open manifolds" Topology , 6 (1966) pp. 171–206