Neyman structure
A structure determined by a statistic that is independent of a sufficient statistic. The concept was introduced by J. Neyman (see [1]) in connection with the problem of constructing similar tests (cf. Similar test) in the theory of statistical hypothesis testing, and the term "Neyman structure" is used when referring to the structure of a statistical test if its critical function has Neyman structure. Suppose that in the realization of a random variable 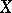 taking values in a sample space
taking values in a sample space 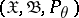 ,
, 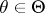 , it is required to verify a composite hypothesis
, it is required to verify a composite hypothesis 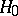 :
: 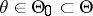 and that for the family
and that for the family 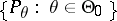 there exists a sufficient statistic
there exists a sufficient statistic 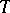 with distribution in the family
with distribution in the family 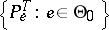 . Then any statistical test of level
. Then any statistical test of level  intended for testing
intended for testing 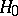 has Neyman structure if its critical function
has Neyman structure if its critical function 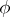 satisfies the condition:
satisfies the condition:
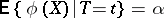 | (1) |
almost everywhere with respect to the measure 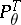 ,
, 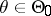 . Evidently, if a statistical test has Neyman structure, then it is similar (cf. Similar test) relative to the family
. Evidently, if a statistical test has Neyman structure, then it is similar (cf. Similar test) relative to the family 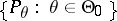 , since
, since
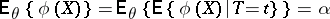 |
for all 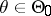 .
.
The validity of (1) essentially reduces the problem of testing the composite hypothesis 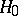 to that of testing
to that of testing 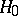 as a simple hypothesis for every fixed value
as a simple hypothesis for every fixed value 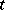 of the sufficient statistic
of the sufficient statistic 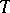 .
.
Example. Suppose that two independent random variables 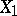 and
and 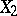 are subject to Poisson laws with unknown parameters
are subject to Poisson laws with unknown parameters 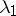 and
and 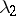 (cf. Poisson distribution) and that the hypothesis
(cf. Poisson distribution) and that the hypothesis 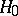 :
:  is to be tested against the alternative
is to be tested against the alternative 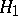 :
: 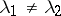 . Thanks to the independence of
. Thanks to the independence of 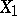 and
and 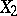 the statistic
the statistic 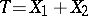 is subject to the Poisson law with parameter
is subject to the Poisson law with parameter 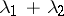 and the conditional distributions of
and the conditional distributions of 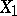 and
and 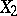 under the condition
under the condition 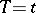 are binomial with parameters
are binomial with parameters  ,
, 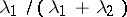 and
and 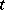 ,
,  , respectively, that is,
, respectively, that is,
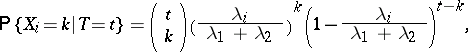 | (2) |
 |
When  is valid, then
is valid, then  is sufficient for the unknown common value
is sufficient for the unknown common value 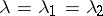 , and from (2) it follows that when
, and from (2) it follows that when 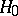 holds, then the conditional distribution of
holds, then the conditional distribution of 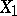 for a fixed value of the sufficient statistic
for a fixed value of the sufficient statistic 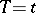 is binomial with parameters
is binomial with parameters 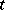 and
and 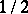 , that is, under
, that is, under 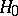 ,
,
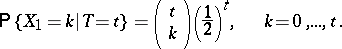 |
Thus, in this case the problem of testing the composite hypothesis 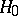 reduces to that of testing the simple hypothesis
reduces to that of testing the simple hypothesis 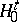 , according to which the conditional distribution of
, according to which the conditional distribution of 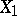 (for a fixed sum
(for a fixed sum 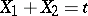 ) is binomial with parameters
) is binomial with parameters 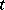 and
and 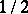 . For testing
. For testing 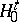 one can use, for example, the sign test.
one can use, for example, the sign test.
The concept of a Neyman structure is of great significance in the problem of testing composite statistical hypotheses, since among the tests having Neyman structure there frequently is a most-powerful test. E. Lehmann and H. Scheffé have shown that a statistical test for testing a composite hypothesis 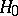 :
: 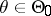 has Neyman structure relative to a sufficient statistic
has Neyman structure relative to a sufficient statistic 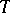 if and only if the family
if and only if the family 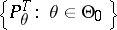 induced by
induced by 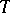 is boundedly complete. On the basis of the concept of a Neyman structure general methods have been worked out for the construction of similar tests. See Distributions, complete family of; Similar test.
is boundedly complete. On the basis of the concept of a Neyman structure general methods have been worked out for the construction of similar tests. See Distributions, complete family of; Similar test.
References
| [1] | J. Neyman, "Current problems of mathematical statistics" , Proc. Internat. Congress Mathematicians (Amsterdam, 1954) , 1 , Noordhoff & North-Holland (1957) pp. 349–370 |
| [2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [3] | Yu.V. Linnik, "Statistical problems with nuisance parameters" , Amer. Math. Soc. (1968) (Translated from Russian) |
Neyman structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Neyman_structure&oldid=14940