Vinogradov estimates

The name of a number of theorems of I.M. Vinogradov. The following ones are the best known.

1) Vinogradov's estimate for character sums (cf. Dirichlet character). If 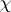is a non-principal character mod 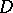, then if , ,

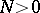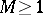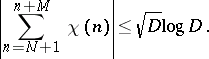2) Vinogradov's estimate for Weyl sums (cf. Weyl sum). Let 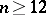be a constant and let 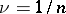. Furthermore, let the points of -dimensional space be subdivided into two classes — class 1 and class 2. A point in class 1 is a point

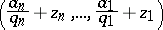where the first terms are rational irreducible fractions with positive denumerators, with lowest common multiple 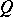which is not larger than 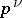, while the second term satisfies the condition

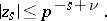A point in class 2 is a point not belonging to class 1. Then, putting

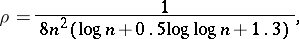for points in class 2,

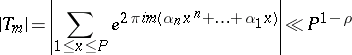if 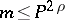. If, on the other hand, one puts

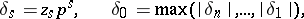then, if 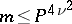, for points of class 1,

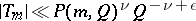or even

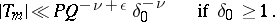3) Vinogradov's estimates for trigonometric sums with prime numbers. Let 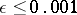. Also, let the points of -dimensional space be subdivided into classes, in accordance with the notation of theorem 2), as follows.

Class 1a comprises those points satisfying the condition

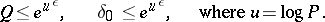Class 1b comprises those points not in class 1a and satisfying the condition

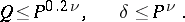Finally, all other points belong to class 2.

For points in class 1a one sets

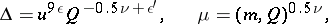or even

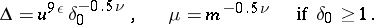For points in class 1b, setting 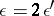, one defines

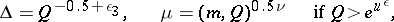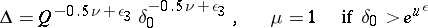(if , , 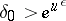any of the above pairs of values of 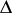and 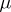may be taken). Finally, one sets

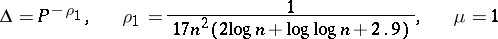for points in class 2. Then

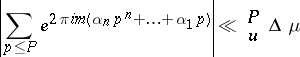if .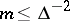

References

[1]	I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian)
[2]	L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1)