Difference set
complete difference set
A set 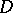 consisting of
consisting of 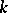 residues
residues 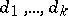 modulo a certain natural number
modulo a certain natural number  such that for each
such that for each 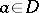 ,
, 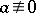 (
(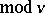 ), there exist precisely
), there exist precisely 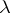 ordered pairs
ordered pairs 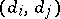 of elements from
of elements from 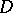 for which
for which
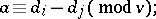 |
the numbers 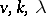 are called the parameters of the difference set. For example, the set
are called the parameters of the difference set. For example, the set 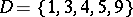 of residues modulo 11 is a difference set with
of residues modulo 11 is a difference set with 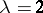 .
.
Difference sets are closely connected with block designs (cf. Block design), namely: The existence of a difference set is equivalent to the existence of a symmetric block design with parameters 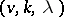 having a cyclic group of automorphisms of order
having a cyclic group of automorphisms of order  (the blocks of such a design are the sets
(the blocks of such a design are the sets 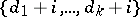 ,
, 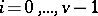 ). The notion of a difference set can be generalized in the following way: A set
). The notion of a difference set can be generalized in the following way: A set 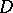 consisting of
consisting of 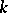 distinct elements
distinct elements 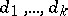 of a group
of a group 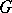 of order
of order  is called a
is called a  -difference set in
-difference set in 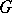 if for any
if for any 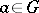 ,
, 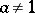 , there exist precisely
, there exist precisely 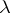 ordered pairs
ordered pairs 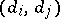 ,
, 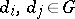 , such that
, such that 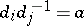 (or, what is the same,
(or, what is the same, 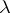 pairs
pairs 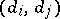 with
with  ). In this case a difference set as defined above is called a cyclic difference set (since the group of residue classes
). In this case a difference set as defined above is called a cyclic difference set (since the group of residue classes 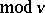 is a cyclic group). The existence of
is a cyclic group). The existence of 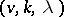 -difference sets in a group
-difference sets in a group 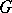 of order
of order  is equivalent to the existence of a symmetric block design with parameters
is equivalent to the existence of a symmetric block design with parameters 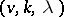 admitting
admitting 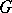 as a regular (that is, without fixed points) group of automorphisms (this design is obtained by identifying the elements of the block design with the elements of the group and the blocks with the sets
as a regular (that is, without fixed points) group of automorphisms (this design is obtained by identifying the elements of the block design with the elements of the group and the blocks with the sets 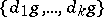 , where
, where 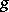 runs over
runs over 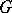 ).
).
The question of the existence and construction of a difference set with given parameters is fundamental in the theory of difference sets. For this question the concept of a multiplier of a difference set turns out to be useful: An automorphism of the group 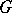 is a multiplier of a
is a multiplier of a 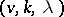 -difference set
-difference set  in
in 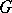 if it is also an automorphism of the block design determined by
if it is also an automorphism of the block design determined by  . For a cyclic difference set a multiplier is a number
. For a cyclic difference set a multiplier is a number 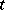 relatively prime with
relatively prime with  and with the property that
and with the property that
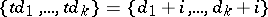 |
for a certain 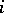 ,
, 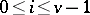 . The multipliers of a cyclic difference set form a group. The following assertion is true: If
. The multipliers of a cyclic difference set form a group. The following assertion is true: If  is a cyclic
is a cyclic 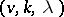 -difference set and if
-difference set and if 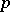 is a prime number dividing
is a prime number dividing 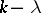 and such that
and such that 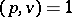 and
and 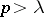 , then
, then 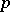 is a multiplier of
is a multiplier of  (the multiplier theorem for difference sets). The following result is useful when constructing difference sets: For any multiplier of a
(the multiplier theorem for difference sets). The following result is useful when constructing difference sets: For any multiplier of a 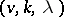 -difference set
-difference set 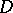 in an Abelian group
in an Abelian group 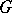 of order
of order  there exists a block in the block design determined by
there exists a block in the block design determined by  which is fixed by this multiplier; when
which is fixed by this multiplier; when  there exists a block fixed by any multiplier.
there exists a block fixed by any multiplier.
Difference sets are usually constructed by direct methods, using the properties of finite fields and cyclotomic fields (see Cyclotomic field) as well as finite geometries. Several infinite families of difference sets are known, for example the following types 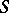 and
and 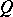 .
.
Type 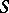 (Singer difference sets): These are hyperplanes in an
(Singer difference sets): These are hyperplanes in an  -dimensional projective geometry over a field of
-dimensional projective geometry over a field of 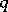 elements. The parameters are:
elements. The parameters are:
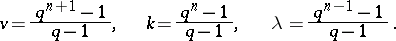 |
Type 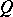 : Quadratic residues in the field
: Quadratic residues in the field 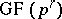 when
when 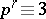 (
(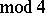 ) (
) (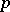 is a prime number). The parameters are:
is a prime number). The parameters are:
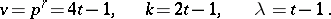 |
For other infinite families of difference sets see [1]–[3]. Besides these difference sets, generalized difference sets are often considered. They are also called difference families and are sets 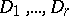 consisting of residues
consisting of residues 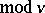 such that for any
such that for any 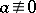 (
(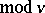 ) there exist precisely
) there exist precisely 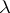 ordered pairs
ordered pairs 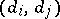 ,
, 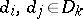 , with
, with
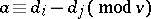 |
for a certain  ,
, 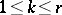 .
.
There are also other generalizations of difference sets.
References
| [1] | M. Hall, "Combinatorial theory" , Blaisdell (1967) |
| [2] | L.D. Baumert, "Cyclic difference sets" , Springer (1971) |
| [3] | M. Hall, "Difference sets" , Combinatorics. 3 Combinatorial group theory. Proc. NATO, Breukelen , Math. Centre Tracts , 57 , CWI (1974) pp. 1–26 |
Difference set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Difference_set&oldid=14897