Arithmetic genus
A numerical invariant of algebraic varieties (cf. Algebraic variety). For an arbitrary projective variety  (over a field
(over a field  ) all irreducible components of which have dimension
) all irreducible components of which have dimension  , and which is defined by a homogeneous ideal
, and which is defined by a homogeneous ideal 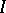 in the ring
in the ring  , the arithmetic genus
, the arithmetic genus  is expressed using the constant term
is expressed using the constant term  of the Hilbert polynomial
of the Hilbert polynomial  of
of  by the formula
by the formula
 |
This classical definition is due to F. Severi [1]. In the general case it is equivalent to the following definition:
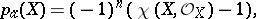 |
where
 |
is the Euler characteristic of the variety 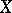 with coefficients in the structure sheaf
with coefficients in the structure sheaf 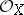 . In this form the definition of the arithmetic genus can be applied to any complete algebraic variety, and this definition also shows the invariance of
. In this form the definition of the arithmetic genus can be applied to any complete algebraic variety, and this definition also shows the invariance of 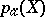 relative to biregular mappings. If
relative to biregular mappings. If 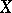 is a non-singular connected variety, and
is a non-singular connected variety, and  is the field of complex numbers, then
is the field of complex numbers, then
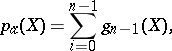 |
where 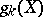 is the dimension of the space of regular differential
is the dimension of the space of regular differential 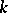 -forms on
-forms on 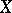 . Such a definition for
. Such a definition for 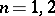 was given by the school of Italian geometers. For example, if
was given by the school of Italian geometers. For example, if 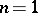 , then
, then 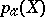 is the genus of the curve
is the genus of the curve  ; if
; if 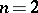 ,
,
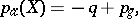 |
where 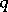 is the irregularity of the surface
is the irregularity of the surface  , while
, while  is the geometric genus of
is the geometric genus of 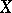 .
.
For any divisor 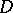 on a normal variety
on a normal variety 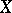 , O. Zariski (see [1]) defined the virtual arithmetic genus
, O. Zariski (see [1]) defined the virtual arithmetic genus 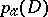 as the constant term of the Hilbert polynomial of the coherent sheaf
as the constant term of the Hilbert polynomial of the coherent sheaf 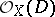 corresponding to
corresponding to  . If the divisors
. If the divisors 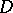 and
and 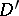 are algebraically equivalent, one has
are algebraically equivalent, one has
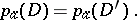 |
The arithmetic genus is a birational invariant in the case of a field  of characteristic zero; in the general case this has so far (1977) been proved for dimensions
of characteristic zero; in the general case this has so far (1977) been proved for dimensions 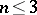 only.
only.
References
| [1] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [2] | F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) |
Arithmetic genus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arithmetic_genus&oldid=14873