Quasi-simple representation
A continuous linear representation 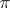 of a connected semi-simple real Lie group
of a connected semi-simple real Lie group 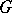 in a Banach space
in a Banach space  such that: 1) the operator
such that: 1) the operator 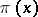 is a scalar multiple of the identity operator on
is a scalar multiple of the identity operator on 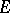 for any
for any  in the centre of
in the centre of 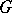 ; and 2) if
; and 2) if 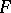 is the space of analytic vectors (cf. Analytic vector) in
is the space of analytic vectors (cf. Analytic vector) in 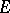 with respect to
with respect to 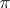 and if
and if 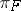 is the representation of the universal enveloping Lie algebra
is the representation of the universal enveloping Lie algebra  of
of 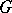 in
in 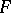 (cf. Universal enveloping algebra), then
(cf. Universal enveloping algebra), then 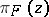 is a scalar multiple of the identity operator on
is a scalar multiple of the identity operator on 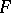 for all
for all  in the centre of
in the centre of 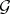 . These scalar multiples determine a character of the centre of
. These scalar multiples determine a character of the centre of 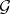 , called the infinitesimal character of the quasi-simple representation. Two quasi-simple representations are said to be infinitesimally equivalent if they determine equivalent representations in the respective vector spaces of analytic vectors of the universal enveloping algebras. Every completely-irreducible representation of a group in a Banach space is a quasi-simple representation, and any irreducible quasi-simple representation of a group
, called the infinitesimal character of the quasi-simple representation. Two quasi-simple representations are said to be infinitesimally equivalent if they determine equivalent representations in the respective vector spaces of analytic vectors of the universal enveloping algebras. Every completely-irreducible representation of a group in a Banach space is a quasi-simple representation, and any irreducible quasi-simple representation of a group 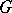 in a Banach space is infinitesimally equivalent to a completely-irreducible representation; the latter is the restriction to the invariant subspace of some quotient representation of the representation (generally non-unitary) in the fundamental series of representations of
in a Banach space is infinitesimally equivalent to a completely-irreducible representation; the latter is the restriction to the invariant subspace of some quotient representation of the representation (generally non-unitary) in the fundamental series of representations of 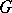 .
.
References
| [1a] | Harish-Chandra, "Representations of a semisimple Lie group on a Banach space I" Trans. Amer. Math. Soc. , 75 (1953) pp. 185–243 |
| [1b] | Harish-Chandra, "Representations of a semisimple Lie groups II" Trans. Amer. Math. Soc. , 76 (1954) pp. 26–65 |
| [2] | J. Lepowsky, "Algebraic results on representations of semisimple Lie groups" Trans. Amer. Math. Soc. , 176 (1973) pp. 1–44 |
| [3] | A.I. Fomin, "Characters of irreducible representations of real semisimple Lie groups" Funct. Anal. Appl. , 10 : 3 (1976) pp. 246–247 Funktsional. Anal. Prilozhen. , 10 : 3 (1976) pp. 95–96 |
Comments
References
| [a1] | N.R. Wallach, "Real reductive groups" , Acad. Press (1988) |
Quasi-simple representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-simple_representation&oldid=14861