Parabolic regression
polynomial regression
A regression model in which the regression functions are polynomials. More precisely, let 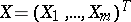 and
and 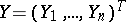 be random vectors taking values
be random vectors taking values 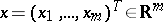 and
and 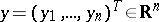 , and suppose that
, and suppose that
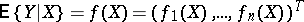 |
exists (i.e. suppose that 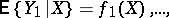
 exist). The regression is called parabolic (polynomial) if the components of the vector
exist). The regression is called parabolic (polynomial) if the components of the vector  are polynomial functions in the components of the vector
are polynomial functions in the components of the vector  . For example, in the elementary case where
. For example, in the elementary case where 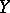 and
and 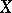 are ordinary random variables, a polynomial regression equation is of the form
are ordinary random variables, a polynomial regression equation is of the form
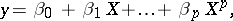 |
where 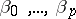 are the regression coefficients. A special case of parabolic regression is linear regression. By adding new components to the vector
are the regression coefficients. A special case of parabolic regression is linear regression. By adding new components to the vector 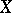 , it is always possible to reduce parabolic regression to linear regression. See Regression; Regression analysis.
, it is always possible to reduce parabolic regression to linear regression. See Regression; Regression analysis.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | G.A.F. Seber, "Linear regression analysis" , Wiley (1977) |
Comments
The phrase "parabolic regression" is seldom used in the Western literature; one uses "polynomial regression" almost exclusively.
Parabolic regression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic_regression&oldid=14841