Baily-Borel compactification
Satake–Baily–Borel compactification
Let  be a semi-simple linear algebraic group (cf. also Semi-simple algebraic group) defined over
be a semi-simple linear algebraic group (cf. also Semi-simple algebraic group) defined over  , meaning that
, meaning that  can be embedded as a subgroup of
can be embedded as a subgroup of  such that each element is diagonalizable (cf. also Diagonalizable algebraic group), and that the equations defining
such that each element is diagonalizable (cf. also Diagonalizable algebraic group), and that the equations defining  as an algebraic variety have coefficients in
as an algebraic variety have coefficients in  (and that the group operation is an algebraic morphism). Further, suppose
(and that the group operation is an algebraic morphism). Further, suppose  contains a torus (cf. Algebraic torus) that splits over
contains a torus (cf. Algebraic torus) that splits over  (i.e.,
(i.e.,  has
has 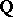 -rank at least one), and
-rank at least one), and 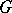 is of Hermitian type, so that
is of Hermitian type, so that 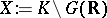 can be given a complex structure with which it becomes a symmetric domain, where
can be given a complex structure with which it becomes a symmetric domain, where 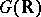 denotes the real points of
denotes the real points of 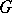 and
and 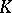 is a maximal compact subgroup. Finally, let
is a maximal compact subgroup. Finally, let  be an arithmetic subgroup (cf. Arithmetic group) of
be an arithmetic subgroup (cf. Arithmetic group) of 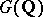 , commensurable with the integer points of
, commensurable with the integer points of 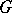 . Then the arithmetic quotient
. Then the arithmetic quotient 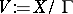 is a normal analytic space whose Baily–Borel compactification, also sometimes called the Satake–Baily–Borel compactification, is a canonically determined projective normal algebraic variety
is a normal analytic space whose Baily–Borel compactification, also sometimes called the Satake–Baily–Borel compactification, is a canonically determined projective normal algebraic variety 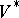 , defined over
, defined over 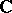 , in which
, in which 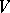 is Zariski-open (cf. also Zariski topology) [a1] [a2] [a15] [a16].
is Zariski-open (cf. also Zariski topology) [a1] [a2] [a15] [a16].
To describe 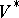 in the complex topology, first note that the Harish–Chandra realization [a6] of
in the complex topology, first note that the Harish–Chandra realization [a6] of 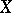 as a bounded symmetric domain may be compactified by taking its topological closure. Then a rational boundary component of
as a bounded symmetric domain may be compactified by taking its topological closure. Then a rational boundary component of 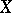 is a boundary component whose stabilizer in
is a boundary component whose stabilizer in 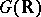 is defined over
is defined over 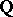 ; based on a detailed analysis of the
; based on a detailed analysis of the 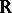 -roots and
-roots and  -roots of
-roots of 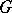 , there is a natural bijection between the rational boundary components of
, there is a natural bijection between the rational boundary components of 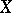 and the proper maximal parabolic subgroups of
and the proper maximal parabolic subgroups of 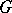 defined over
defined over 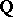 . Let
. Let  denote the union of
denote the union of 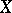 with all its rational boundary components. Then (cf. [a18]) there is a unique topology, the Satake topology, on
with all its rational boundary components. Then (cf. [a18]) there is a unique topology, the Satake topology, on 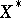 such that the action of
such that the action of 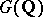 extends continuously and
extends continuously and 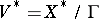 with its quotient topology compact and Hausdorff. It also follows from the construction that
with its quotient topology compact and Hausdorff. It also follows from the construction that 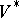 is a finite disjoint union of the form
is a finite disjoint union of the form
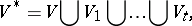 |
where 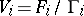 for some rational boundary component
for some rational boundary component 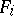 of
of  , and
, and  is the intersection of
is the intersection of 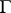 with the stabilizer of
with the stabilizer of 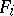 . In addition,
. In addition, 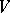 and each
and each 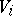 has a natural structure as a normal analytic space; the closure of any
has a natural structure as a normal analytic space; the closure of any 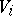 is the union of
is the union of 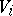 with some
with some 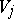 s of strictly smaller dimension; and it can be proved that every point
s of strictly smaller dimension; and it can be proved that every point 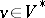 has a fundamental system of neighbourhoods
has a fundamental system of neighbourhoods  such that
such that 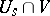 is connected for every
is connected for every  .
.
In order to describe the structure sheaf of 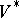 (cf. also Scheme) with which it becomes a normal analytic space and a projective variety, define an
(cf. also Scheme) with which it becomes a normal analytic space and a projective variety, define an 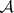 -function on an open subset
-function on an open subset 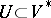 to be a continuous complex-valued function on
to be a continuous complex-valued function on 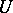 whose restriction to
whose restriction to 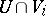 is analytic,
is analytic, 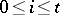 , where
, where 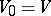 . Then, associating to each open
. Then, associating to each open 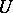 the
the 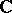 -module of
-module of 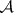 -functions on
-functions on  determines the sheaf
determines the sheaf 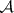 of germs of
of germs of 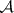 -functions. Further, for each
-functions. Further, for each  the sheaf of germs of restrictions of
the sheaf of germs of restrictions of 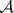 -functions to
-functions to 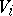 is the structure sheaf of
is the structure sheaf of 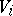 . Ultimately it is proved [a2] that
. Ultimately it is proved [a2] that 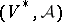 is a normal analytic space which can be embedded in some complex projective space as a projective, normal algebraic variety. The proof of this last statement depends on exhibiting that in the collection of
is a normal analytic space which can be embedded in some complex projective space as a projective, normal algebraic variety. The proof of this last statement depends on exhibiting that in the collection of  -functions there are enough automorphic forms for
-functions there are enough automorphic forms for  , more specifically, Poincaré-Eisenstein series, which generalize both Poincaré series and Eisenstein series (cf. also Theta-series), to separate points on
, more specifically, Poincaré-Eisenstein series, which generalize both Poincaré series and Eisenstein series (cf. also Theta-series), to separate points on  as well as to provide a projective embedding.
as well as to provide a projective embedding.
History and examples.
The simplest example of a Baily–Borel compactification is when 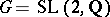 , and
, and 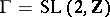 , and
, and  is the complex upper half-plane, on which
is the complex upper half-plane, on which  in
in 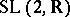 acts by
acts by 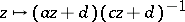 . (The bounded realization of
. (The bounded realization of 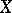 is a unit disc, to which the upper half-plane maps by
is a unit disc, to which the upper half-plane maps by 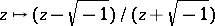 .) The properly discontinuous action of
.) The properly discontinuous action of 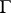 on
on  extends to
extends to 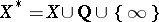 , and
, and 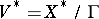 is a smooth projective curve. Since
is a smooth projective curve. Since 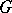 has
has 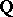 -rank one,
-rank one, 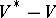 is a finite set of points, referred to as cusps.
is a finite set of points, referred to as cusps.
Historically the next significant example was for the Siegel modular group, with 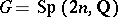 , and
, and 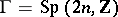 , and
, and 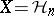 consisting of
consisting of 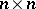 symmetric complex matrices with positive-definite imaginary part; here
symmetric complex matrices with positive-definite imaginary part; here 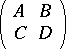 in
in 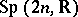 acts on
acts on 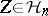 by
by 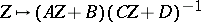 . I. Satake [a17] was the first to describe a compactification of
. I. Satake [a17] was the first to describe a compactification of 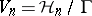 as
as 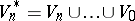 endowed with its Satake topology (cf. also Satake compactification). Then Satake, H. Cartan and others (in [a19]) and W.L. Baily [a13] further investigated and exhibited the analytic and algebraic structure of
endowed with its Satake topology (cf. also Satake compactification). Then Satake, H. Cartan and others (in [a19]) and W.L. Baily [a13] further investigated and exhibited the analytic and algebraic structure of 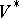 , using automorphic forms as mentioned above. Baily [a14] also treated the Hilbert–Siegel modular group, where
, using automorphic forms as mentioned above. Baily [a14] also treated the Hilbert–Siegel modular group, where 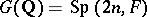 for a totally real number field
for a totally real number field 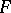 .
.
In the meanwhile, under only some mild assumption about 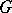 , Satake [a18] constructed
, Satake [a18] constructed 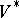 with its Satake topology, while I.I. Piateckii-Shapiro [a10] described a normal analytic compactification whose topology was apparently weaker than that of the Baily–Borel compactification. Later, P. Kiernan [a7] showed that the topology defined by Piateckii-Shapiro is homeomorphic to the Satake topology used by Baily and Borel.
with its Satake topology, while I.I. Piateckii-Shapiro [a10] described a normal analytic compactification whose topology was apparently weaker than that of the Baily–Borel compactification. Later, P. Kiernan [a7] showed that the topology defined by Piateckii-Shapiro is homeomorphic to the Satake topology used by Baily and Borel.
Other compactifications.
Other approaches to the compactification of arithmetic quotients of symmetric domains to which the Satake and Baily–Borel approach may be compared are the Borel–Serre compactification [a3], see the discussion in [a20], and the method of toroidal embeddings [a12].
Cohomology.
Zucker's conjecture [a21] that the (middle perversity) intersection cohomology [a4] (cf. also Intersection homology) of the Baily–Borel compactification coincides with its 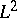 -cohomology, has been given two independent proofs (see [a8] and [a11]); see also the discussion and bibliography in [a5].
-cohomology, has been given two independent proofs (see [a8] and [a11]); see also the discussion and bibliography in [a5].
Arithmetic and moduli.
In many cases 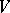 has an interpretation as the moduli space for some family of Abelian varieties (cf. also Moduli theory), usually with some additional structure; this leads to the subject of Shimura varieties (cf. also Shimura variety), which also addresses arithmetic questions such as the field of definition of
has an interpretation as the moduli space for some family of Abelian varieties (cf. also Moduli theory), usually with some additional structure; this leads to the subject of Shimura varieties (cf. also Shimura variety), which also addresses arithmetic questions such as the field of definition of 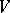 and
and 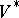 . Geometrically, the strata of
. Geometrically, the strata of 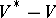 parameterize different semi-Abelian varieties, i.e., semi-direct products of algebraic tori with Abelian varieties, into which the Abelian varieties represented by points on
parameterize different semi-Abelian varieties, i.e., semi-direct products of algebraic tori with Abelian varieties, into which the Abelian varieties represented by points on 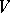 degenerate. For an example see [a9], where this is thoroughly worked out for
degenerate. For an example see [a9], where this is thoroughly worked out for 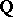 -forms of
-forms of  , especially for
, especially for 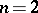 .
.
References
| [a1] | W.L. Baily, Jr., A. Borel, "On the compactification of arithmetically defined quotients of bounded symmetric domains" Bull. Amer. Math. Soc. , 70 (1964) pp. 588–593 |
| [a2] | W.L. Baily, Jr., A. Borel, "Compactification of arithmetic quotients of bounded symmetric domains" Ann. of Math. (2) , 84 (1966) pp. 442–528 |
| [a3] | A. Borel, J.P. Serre, "Corners and arithmetic groups" Comment. Math. Helv. , 48 (1973) pp. 436–491 |
| [a4] | M. Goresky, R. MacPherson, "Intersection homology, II" Invent. Math. , 72 (1983) pp. 135–162 |
| [a5] | M. Goresky, "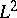 -cohomology is intersection cohomology" R.P. Langlands (ed.) D. Ramakrishnan (ed.) , The Zeta Functions of Picard Modular Surfaces , Publ. CRM (1992) pp. 47–63 -cohomology is intersection cohomology" R.P. Langlands (ed.) D. Ramakrishnan (ed.) , The Zeta Functions of Picard Modular Surfaces , Publ. CRM (1992) pp. 47–63 |
| [a6] | Harish-Chandra, "Representations of semi-simple Lie groups. VI" Amer. J. Math. , 78 (1956) pp. 564–628 |
| [a7] | P. Kiernan, "On the compactifications of arithmetic quotients of symmetric spaces" Bull. Amer. Math. Soc. , 80 (1974) pp. 109–110 |
| [a8] | E. Looijenga, "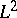 -cohomology of locally symmetric varieties" Computers Math. , 67 (1988) pp. 3–20 -cohomology of locally symmetric varieties" Computers Math. , 67 (1988) pp. 3–20 |
| [a9] | "The zeta functions of Picard modular surfaces" R.P. Langlands (ed.) D. Ramakrishnan (ed.) , Publ. CRM (1992) |
| [a10] | I.I. Piateckii-Shapiro, "Arithmetic groups in complex domains" Russian Math. Surveys , 19 (1964) pp. 83–109 Uspekhi Mat. Nauk. , 19 (1964) pp. 93–121 |
| [a11] | L. Saper, M. Stern, "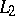 -cohomology of arithmetic varieties" Ann. of Math. , 132 : 2 (1990) pp. 1–69 -cohomology of arithmetic varieties" Ann. of Math. , 132 : 2 (1990) pp. 1–69 |
| [a12] | A. Ash, D. Mumford, M. Rapoport, Y. Tai, "Smooth compactifications of locally symmetric varieties" , Math. Sci. Press (1975) |
| [a13] | W.L. Baily, Jr., "On Satake's compactification of 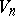 " Amer. J. Math. , 80 (1958) pp. 348–364 " Amer. J. Math. , 80 (1958) pp. 348–364 |
| [a14] | W.L. Baily, Jr., "On the Hilbert–Siegel modular space" Amer. J. Math. , 81 (1959) pp. 846–874 |
| [a15] | W.L. Baily, Jr., "On the orbit spaces of arithmetic groups" , Arithmetical Algebraic Geometry (Proc. Conf. Purdue Univ., 1963) , Harper and Row (1965) pp. 4–10 |
| [a16] | W.L. Baily, Jr., "On compactifications of orbit spaces of arithmetic discontinuous groups acting on bounded symmetric domains" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 281–295 |
| [a17] | I. Satake, "On the compactification of the Siegel space" J. Indian Math. Soc. (N.S.) , 20 (1956) pp. 259–281 |
| [a18] | I. Satake, "On compactifications of the quotient spaces for arithmetically defined discontinuous groups" Ann. of Math. , 72 : 2 (1960) pp. 555–580 |
| [a19] | "Fonctions automorphes" , Sém. H. Cartan 10ième ann. (1957/8) , 1–2 , Secr. Math. Paris (1958) (Cartan) |
| [a20] | S. Zucker, "Satake compactifications" Comment. Math. Helv. , 58 (1983) pp. 312–343 |
| [a21] | S. Zucker, "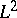 -cohomology of warped products and arithmetic groups" Ann. of Math. , 70 (1982) pp. 169–218 -cohomology of warped products and arithmetic groups" Ann. of Math. , 70 (1982) pp. 169–218 |
Baily-Borel compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baily-Borel_compactification&oldid=14832