O'Nan-Scott theorem
A reduction theorem for the class of finite primitive permutation groups, distributing them in subclasses called types whose number and definition may vary slightly according to the criteria used and the order in which these are applied. Below, six types are described by characteristic properties, additional properties are given, a converse group-theoretical construction is presented, and a few small examples are given.
Let  be a finite set and let
be a finite set and let  be a primitive permutation group on
be a primitive permutation group on  . Then the stabilizer
. Then the stabilizer  of a point
of a point 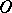 belonging to
belonging to  is a maximal subgroup of
is a maximal subgroup of 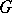 containing no non-trivial normal subgroup of
containing no non-trivial normal subgroup of 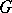 . Conversely, and constructively, this amounts to the data of a group
. Conversely, and constructively, this amounts to the data of a group  and of a maximal subgroup
and of a maximal subgroup 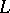 containing no non-trivial normal subgroup of
containing no non-trivial normal subgroup of 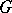 ; the elements of
; the elements of  are the left cosets
are the left cosets 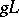 with
with  in
in 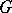 , and the action of
, and the action of 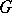 on
on  is by left translation.
is by left translation.
The reduction is based on a minimal normal subgroup 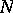 of
of 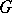 . Either
. Either 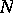 is unique or there are two such, each being regular on
is unique or there are two such, each being regular on  and centralizing the other (cf. also Centralizer). The socle,
and centralizing the other (cf. also Centralizer). The socle,  , of
, of 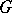 is the direct product of those two subgroups. The subgroup
is the direct product of those two subgroups. The subgroup  is a direct product of isomorphic copies of a simple group
is a direct product of isomorphic copies of a simple group 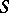 , hence
, hence 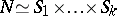 with
with 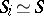 for
for 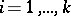 and
and  . One puts
. One puts 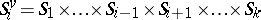 ,
, 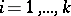 . Fixing a point
. Fixing a point  of
of  , let
, let  be the orbit of
be the orbit of  under
under 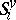 and let
and let 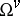 be the intersection of the
be the intersection of the 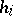 ,
, 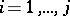 .
.
One of the criteria of the reduction is whether 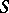 is Abelian or not (cf. Abelian group), and another is to distinguish the case
is Abelian or not (cf. Abelian group), and another is to distinguish the case 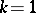 from
from 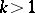 . Still another criterion is to distinguish the case where
. Still another criterion is to distinguish the case where 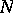 is regular or not. If
is regular or not. If  is non-Abelian, then
is non-Abelian, then 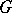 acts transitively on the set
acts transitively on the set 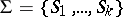 and it induces a permutation group
and it induces a permutation group 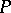 on it with
on it with  in the kernel of the action. The nature of
in the kernel of the action. The nature of 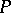 provides another property. A final property is whether
provides another property. A final property is whether 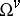 is reduced to
is reduced to  or equal to
or equal to  . The affine type is characterized by the fact that
. The affine type is characterized by the fact that 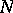 is unique and Abelian. Then
is unique and Abelian. Then  is endowed with a structure of an affine geometry
is endowed with a structure of an affine geometry 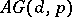 whose points are the elements of
whose points are the elements of  ,
, 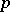 is a prime number and
is a prime number and  is the dimension, with
is the dimension, with 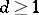 . Thus
. Thus 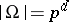 and
and  is a subgroup of the affine group
is a subgroup of the affine group 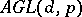 containing the group
containing the group  of all translations. Also, the stabilizer
of all translations. Also, the stabilizer 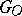 of
of 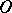 is an irreducible subgroup (cf. also Irreducible matrix group) of
is an irreducible subgroup (cf. also Irreducible matrix group) of 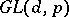 .
.
Conversely, for a finite vector space of dimension 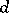 over the prime field of order
over the prime field of order  and an irreducible subgroup
and an irreducible subgroup  of
of  , the extension of
, the extension of 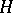 by the translations provides a primitive permutation group of affine type.
by the translations provides a primitive permutation group of affine type.
Examples are the symmetric and alternating groups of degree less than or equal to four (cf. Symmetric group; Alternating group), and the groups  where
where 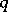 is a prime power.
is a prime power.
The almost-simple type is characterized by 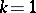 ,
, 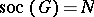 , and
, and 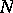 non-Abelian. It follows that
non-Abelian. It follows that 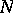 is not regular and that
is not regular and that 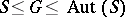 ; namely,
; namely,  is isomorphic to an almost-simple group.
is isomorphic to an almost-simple group.
Conversely, the data of an almost-simple group and one of its maximal subgroups not containing its non-Abelian simple socle determines a primitive group of almost-simple type.
Examples are the symmetric and alternating groups of degree  (cf. Symmetric group; Alternating group), the group
(cf. Symmetric group; Alternating group), the group 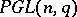 acting on the projective subspaces of a fixed dimension, etc.
acting on the projective subspaces of a fixed dimension, etc.
The holomorphic simple type is characterized by 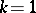 and the fact that there are two non-Abelian regular minimal normal subgroups. Moreover,
and the fact that there are two non-Abelian regular minimal normal subgroups. Moreover,  , and
, and 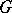 is described as the set of mappings from
is described as the set of mappings from 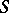 onto
onto 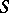 of the form
of the form 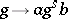 , where
, where 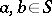 and
and  varies in some subgroup of
varies in some subgroup of 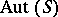 . Conversely, for any non-Abelian simple group
. Conversely, for any non-Abelian simple group  the action on the set of elements of
the action on the set of elements of 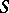 provided by the mappings
provided by the mappings  , where
, where 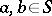 and
and  varies in some subgroup of
varies in some subgroup of 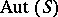 , gives a primitive group of holomorphic simple type.
, gives a primitive group of holomorphic simple type.
Examples occur for the degree 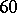 with
with  , for the degree
, for the degree 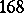 with
with  , etc.
, etc.
The twisted wreath product type is characterized by the fact of 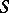 being non-Abelian,
being non-Abelian, 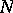 being regular and unique. Then
being regular and unique. Then 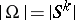 ,
, 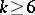 . The stabilizer
. The stabilizer 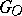 is isomorphic to some transitive group of degree
is isomorphic to some transitive group of degree 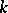 whose point stabilizer has a composition factor isomorphic to
whose point stabilizer has a composition factor isomorphic to 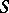 . The smallest example has degree
. The smallest example has degree 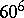 with
with 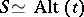 .
.
A converse construction is not attempted here.
For the next descriptions of types some preliminary notation and terminology is needed.
Let 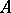 be a set of cardinality
be a set of cardinality 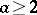 and let
and let 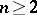 be some integer. Consider the Cartesian product, or, better, the Cartesian geometry, which is the set
be some integer. Consider the Cartesian product, or, better, the Cartesian geometry, which is the set 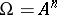 equipped with the obvious Cartesian subspaces obtained by the requirement that some coordinates take constant values, and with the obvious Cartesian parallelism. Each class of parallels is a partition of
equipped with the obvious Cartesian subspaces obtained by the requirement that some coordinates take constant values, and with the obvious Cartesian parallelism. Each class of parallels is a partition of  . If
. If 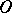 is a point of
is a point of  , then there are
, then there are  Cartesian hyperplanes containing
Cartesian hyperplanes containing 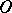 and each of the
and each of the 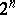 Cartesian subspaces containing
Cartesian subspaces containing 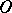 corresponds to a unique subset of that set of hyperplanes.
corresponds to a unique subset of that set of hyperplanes. 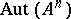 denotes the automorphism group. For a fixed coordinate
denotes the automorphism group. For a fixed coordinate 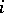 (
(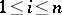 ) there is a subgroup
) there is a subgroup 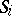 of
of 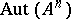 fixing each coordinate except
fixing each coordinate except 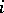 , and
, and 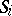 is isomorphic to the symmetric group of degree
is isomorphic to the symmetric group of degree  . The direct product
. The direct product  is the automorphism group mapping each Cartesian subspace to one of its parallels. Also,
is the automorphism group mapping each Cartesian subspace to one of its parallels. Also, 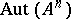 induces the symmetric group of degree
induces the symmetric group of degree  on the set
on the set 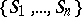 .
.
The product action of a wreath product type is characterized by 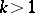 ,
, 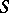 non-Abelian and
non-Abelian and 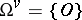 . Then
. Then 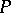 is primitive. Also,
is primitive. Also, 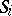 is intransitive, the set
is intransitive, the set  bears the structure of a Cartesian geometry invariant under
bears the structure of a Cartesian geometry invariant under 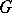 and whose Cartesian hyperplanes are the
and whose Cartesian hyperplanes are the 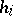 and their transforms under
and their transforms under 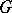 , and
, and 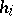 is parallel to its transforms under
is parallel to its transforms under 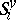 . Each
. Each 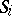 leaves each Cartesian line in some parallel class invariant. The group stabilizing a Cartesian line induces on it some primitive group with
leaves each Cartesian line in some parallel class invariant. The group stabilizing a Cartesian line induces on it some primitive group with 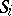 as minimal normal subgroup, which is a group of almost-simple type or of holomorphic simple type. The distinction between these two cases is characterized by
as minimal normal subgroup, which is a group of almost-simple type or of holomorphic simple type. The distinction between these two cases is characterized by 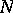 being not regular or being regular, respectively.
being not regular or being regular, respectively.
Conversely, given a primitive group 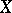 of almost-simple type or holomorphic simple type with minimal normal subgroup
of almost-simple type or holomorphic simple type with minimal normal subgroup 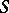 on the set
on the set 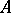 and a primitive group
and a primitive group 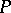 of degree
of degree 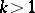 , these data provide a wreath product group
, these data provide a wreath product group 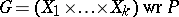 with a product action on the Cartesian geometry
with a product action on the Cartesian geometry 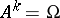 , in which
, in which 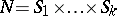 is a minimal normal subgroup of
is a minimal normal subgroup of 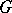 and the
and the 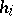 are the Cartesian hyperplanes of
are the Cartesian hyperplanes of  containing a given point.
containing a given point.
Examples occur for 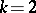 ,
, 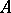 of cardinality five and
of cardinality five and 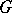 equal to
equal to 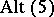 or
or 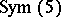 ; also, for
; also, for 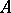 of cardinality six and
of cardinality six and 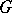 one of
one of 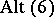 or
or 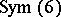 , etc.
, etc.
The diagonal type is characterized by the fact 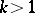 ,
,  is non-Abelian,
is non-Abelian, 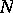 is not regular, and
is not regular, and  . Then
. Then 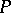 is primitive. Also, each
is primitive. Also, each 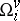 is transitive on
is transitive on  and
and 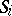 is semi-regular. Moreover,
is semi-regular. Moreover, 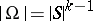 ,
, 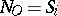 and
and 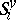 is regular for all
is regular for all 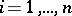 . Let a "line" be any orbit of some
. Let a "line" be any orbit of some  . Call two lines "parallel" if they are orbits of the same
. Call two lines "parallel" if they are orbits of the same  . For each
. For each 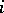 , the lines that are not orbits of
, the lines that are not orbits of 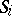 constitute the Cartesian lines of a Cartesian space of dimension
constitute the Cartesian lines of a Cartesian space of dimension 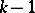 on
on  . This geometric structure is called a diagonal space.
. This geometric structure is called a diagonal space.
A converse construction is not given here. The smallest examples occur for 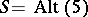 and
and 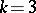 , hence for
, hence for 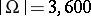 .
.
See also: Permutation group; Primitive group of permutations; Symmetric group; Simple group; Wreath product.
References
| [a1] | M. Aschbacher, "The subgroup structure of the finite classical groups by Peter Kleidman and Martin Liebeck" Bull. Amer. Math. Soc. , 25 (1991) pp. 200–204 |
| [a2] | F. Buekenhout, "On a theorem of O'Nan and Scott" Bull. Soc. Math. Belg. B , 40 (1988) pp. 1–9 |
| [a3] | J.D. Dixon, B. Mortimer, "Permutation groups" , GTM , Springer (1996) |
O'Nan-Scott theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=O%27Nan-Scott_theorem&oldid=14822