Hasse invariant
The Hasse invariant 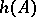 of a central simple algebra
of a central simple algebra  over a local field
over a local field  (or over the field
(or over the field 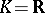 or
or 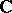 ) is the image of the class of
) is the image of the class of 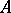 under the canonical isomorphism of the Brauer group of
under the canonical isomorphism of the Brauer group of 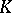 onto the group of all complex roots of unity (or onto the group
onto the group of all complex roots of unity (or onto the group 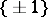 or
or 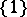 ). For a cyclic algebra
). For a cyclic algebra 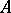 with generators
with generators 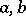 and defining relations
and defining relations 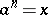 ,
, 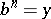 ,
, 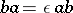 , where
, where 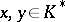 and
and 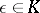 is a primitive
is a primitive  -th root of unity, the Hasse invariant
-th root of unity, the Hasse invariant 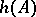 is the same as the norm-residue symbol (Hilbert symbol)
is the same as the norm-residue symbol (Hilbert symbol) 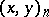 . In particular, the Hasse invariant of the quaternion algebra is
. In particular, the Hasse invariant of the quaternion algebra is 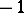 .
.
For a central algebra 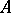 over a global field
over a global field  and any valuation
and any valuation  of this field the local Hasse invariant
of this field the local Hasse invariant 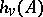 is defined as the Hasse invariant of the algebra
is defined as the Hasse invariant of the algebra 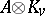 over the completion
over the completion 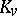 of
of 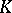 in the topology determined by
in the topology determined by  . The local Hasse invariants determine the class of
. The local Hasse invariants determine the class of 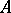 uniquely. They are related by the following conditions: 1) there are only finitely-many valuations
uniquely. They are related by the following conditions: 1) there are only finitely-many valuations  for which
for which 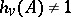 ; and 2)
; and 2) 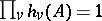 (the reciprocity law). Apart from these conditions they can assume arbitrary values.
(the reciprocity law). Apart from these conditions they can assume arbitrary values.
The Hasse invariant was introduced by H. Hasse [1] and [2].
References
| [1] | H. Hasse, "Ueber 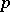 -adische Schiefkörper und ihre Bedeutung für die Arithmetik hyperkomplexen Zahlsysteme" Math. Ann. , 104 (1931) pp. 495–534 -adische Schiefkörper und ihre Bedeutung für die Arithmetik hyperkomplexen Zahlsysteme" Math. Ann. , 104 (1931) pp. 495–534 |
| [2] | H. Hasse, "Die Struktur der R. Brauerschen Algebrenklassengruppe über einem algebraischen Zahlkörper. Inbesondere Begründung der Theorie des Normenrestsymbols und Herleitung des Reziprozitätsgesetzes mit nichtkommutativen Hilfsmitteln" Math. Ann. , 107 (1933) pp. 731–760 |
| [3] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
| [4] | A. Weil, "Basic number theory" , Springer (1967) |
The Hasse invariant, the Hasse–Minkowski invariant, Hasse's symbol, 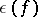 , of a non-degenerate quadratic form
, of a non-degenerate quadratic form  over a local field
over a local field 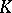 of characteristic
of characteristic 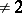 (or over the field
(or over the field 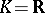 or
or 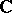 ) is the product
) is the product
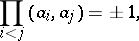 |
where 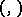 is the quadratic Hilbert symbol, that is,
is the quadratic Hilbert symbol, that is, 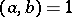 if the quadratic form
if the quadratic form 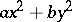 represents 1 in the field
represents 1 in the field 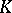 and
and 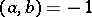 otherwise. The Hasse invariant depends only on the equivalence class of the form
otherwise. The Hasse invariant depends only on the equivalence class of the form 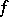 , and not on the choice of a diagonal form in this class. Sometimes the Hasse invariant is defined as the product
, and not on the choice of a diagonal form in this class. Sometimes the Hasse invariant is defined as the product 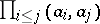 , which differs from the definition above by the factor
, which differs from the definition above by the factor 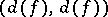 , where
, where 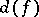 is the discriminant of the form
is the discriminant of the form 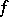 .
.
In the case of a local field 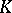 the number
the number  of variables, the discriminant and the Hasse invariant determine the class of the form
of variables, the discriminant and the Hasse invariant determine the class of the form 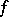 . For
. For 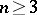 , the invariants
, the invariants 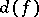 and
and 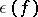 can take arbitrary values independently of each other; for
can take arbitrary values independently of each other; for 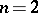 the case
the case 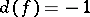 ,
, 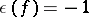 is excluded; for
is excluded; for 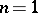 one always has
one always has 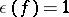 .
.
When 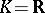 , the Hasse invariant can be expressed in terms of the signature, namely,
, the Hasse invariant can be expressed in terms of the signature, namely,
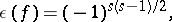 |
where  is the negative index of inertia of the form
is the negative index of inertia of the form 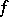 . When
. When 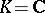 , one has
, one has 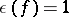 .
.
For a non-degenerate quadratic form 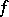 over a global field
over a global field 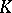 of characteristic
of characteristic 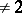 and any valuation
and any valuation  of
of 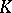 the local Hasse invariant
the local Hasse invariant 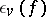 is defined as the Hasse invariant of the quadratic form
is defined as the Hasse invariant of the quadratic form 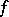 regarded over the completion
regarded over the completion 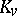 of
of 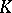 in the topology determined by
in the topology determined by  . The number of variables, the discriminant, the local Hasse invariants, and the signatures over the real completions of
. The number of variables, the discriminant, the local Hasse invariants, and the signatures over the real completions of 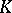 determine the class of
determine the class of 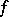 .
.
Necessary and sufficient conditions for the existence of a non-degenerate quadratic form in  variables over a global field
variables over a global field 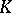 of characteristic
of characteristic 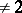 having a given discriminant
having a given discriminant 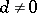 , given the local Hasse invariants
, given the local Hasse invariants 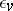 , and, for real valuations
, and, for real valuations  , given the negative indices of inertia
, given the negative indices of inertia 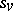 , are as follows:
, are as follows:
a) 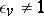 for only finitely-many valuations
for only finitely-many valuations  ;
;
b) 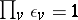 (a consequence of the quadratic reciprocity law);
(a consequence of the quadratic reciprocity law);
c) 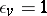 if
if 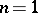 or if
or if 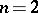 and
and 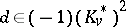 ;
;
d) 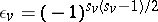 for every real valuation
for every real valuation  ;
;
e) 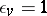 for every complex valuation
for every complex valuation  ;
;
f) 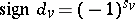 for every real valuation
for every real valuation  (here
(here 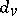 is the image of
is the image of 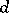 under the isomorphism
under the isomorphism 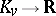 ).
).
The Hasse invariant was introduced by H. Hasse .
References
| [1a] | H. Hasse, "Ueber die Darstellbarkeit von Zahlen durch quadratische Formen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 152 (1923) pp. 129–148 |
| [1b] | H. Hasse, "Ueber die Aequivalenz quadratischer Formen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 152 (1923) pp. 205–224 |
| [1c] | H. Hasse, "Symmetrische Matrizen im Körper der rationalen Zahlen" J. Reine Angew. Math. , 153 (1924) pp. 12–43 |
| [1d] | H. Hasse, "Darstellbarkeit von Zahlen durch quadratische Formen in einem beliebigen algebraischen Zahlkörper" J. Reine Angew. Math. , 153 (1924) pp. 113–130 |
| [1e] | H. Hasse, "Aequivalenz quadratischer Formen in einem beliebigen algebraischen Zahlkörper" J. Reine Angew. Math. , 153 (1924) pp. 158–162 |
| [2] | O.T. O'Meara, "Introduction to quadratic forms" , Springer (1963) |
| [3] | T.Y. Lam, "The algebraic theory of quadratic forms" , Benjamin (1973) |
| [4] | J.W.S. Cassels, "Rational quadratic forms" , Acad. Press (1978) |
The Hasse invariant of an elliptic curve 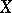 over a field
over a field 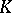 of characteristic
of characteristic 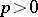 is the number 0 or 1 depending on whether the endomorphism of the cohomology group
is the number 0 or 1 depending on whether the endomorphism of the cohomology group 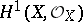 induced by the Frobenius endomorphism of
induced by the Frobenius endomorphism of 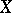 is null or bijective. Curves for which the Hasse invariant is zero are called supersingular.
is null or bijective. Curves for which the Hasse invariant is zero are called supersingular.
References
| [1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
| [2] | Yu.I. Manin, "On the Hasse–Witt matrix of an algebraic curve" Izv. Akad. Nauk. SSSR Ser. Mat. , 25 : 1 (1961) pp. 153–172 (In Russian) |
Comments
References
| [a1] | J.H. Silverman, "The arithmetic of elliptic curves" , Springer (1986) |
Hasse invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hasse_invariant&oldid=14815