Normalizer of a subset
From Encyclopedia of Mathematics
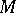 of a group
of a group 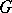 in a subgroup
in a subgroup 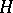 of
of 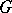
The set
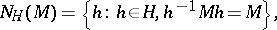 |
that is, the set of all elements 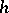 of
of 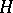 such that
such that 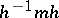 (the conjugate of
(the conjugate of 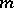 by
by 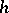 ) for every
) for every 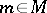 also belongs to
also belongs to 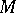 . For any
. For any 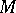 and
and 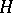 the normalizer
the normalizer 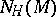 is a subgroup of
is a subgroup of 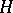 . An important special case is the normalizer of a subgroup of a group
. An important special case is the normalizer of a subgroup of a group 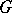 in
in 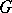 . A subgroup
. A subgroup 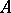 of a group
of a group 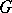 is normal (or invariant, cf. Invariant subgroup) in
is normal (or invariant, cf. Invariant subgroup) in 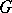 if and only if
if and only if 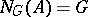 . The normalizer of a set consisting of a single element is the same as its centralizer. For any
. The normalizer of a set consisting of a single element is the same as its centralizer. For any 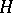 and
and 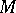 the cardinality of the class of subsets conjugate to
the cardinality of the class of subsets conjugate to 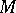 by elements of
by elements of  (that is, subsets of the form
(that is, subsets of the form  ,
, 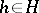 ) is equal to the index
) is equal to the index 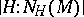 .
.
References
| [1] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) |
Comments
References
| [a1] | D.J.S. Robinson, "A course in the theory of groups" , Springer (1980) |
How to Cite This Entry:
Normalizer of a subset. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normalizer_of_a_subset&oldid=14809
Normalizer of a subset. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normalizer_of_a_subset&oldid=14809
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article