Hurwitz theorem

Let 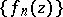be a sequence of holomorphic functions in a domain 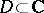that converges uniformly on compact sets in 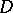to a function 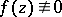. Then, for any closed rectifiable Jordan curve 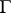lying in 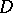together with the domain bounded by 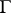and not passing through zeros of 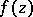, it is possible to find a number 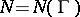such that for 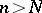each of the functions 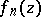has inside 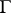the same number of zeros as 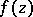inside 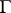. Obtained by A. Hurwitz .

References

[1a]	A. Hurwitz, "Ueber die Bedingungen, unter welchen eine Gleichung nur Würzeln mit negativen reellen Teilen besitzt" Math. Ann. , 46 (1895) pp. 273–284
[1b]	A. Hurwitz, "Ueber die Bedingungen, unter welchen eine Gleichung nur Würzeln mit negativen reellen Teilen besitzt" , Math. Werke , 2 , Birkhäuser (1933) pp. 533–545
[2]	A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian)

Comments

For another theorem using "nearness of functions" to derive "equality of number of zeros" see Rouché theorem.