Lie group, nilpotent

A Lie group that is nilpotent as an abstract group (cf. Nilpotent group). An Abelian Lie group is nilpotent. If 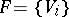is a flag in a finite-dimensional vector space 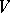over a field 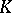, then

is a nilpotent algebraic group over 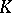; in a basis compatible with 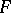its elements are represented by triangular matrices with ones on the main diagonal. If 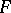is a complete flag (that is, if 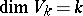), then the matrix nilpotent Lie group 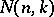corresponding to 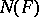consists of all matrices of order 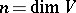of the form mentioned above.

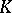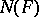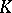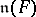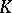If is a complete normed field, then is a nilpotent Lie group over . Its Lie algebra is (see Lie algebra, nilpotent). More generally, the Lie algebra of a Lie group over a field of characteristic 0 is nilpotent if and only if the connected component 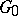of the identity of is nilpotent. This makes it possible to carry over to nilpotent Lie groups the properties of nilpotent Lie algebras (see [2], [4], [5]). The group version of Engel's theorem admits the following strengthening (Kolchin's theorem): If 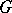is a subgroup of 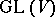, where 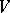is a finite-dimensional vector space over an arbitrary field 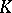, and if every 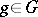is unipotent, then there is a complete flag in 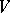such that 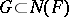(and 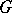automatically turns out to be nilpotent) (see [3]).

Nilpotent Lie groups are solvable, so the properties of solvable Lie groups carry over them, and often in a strengthened from, since every nilpotent Lie group is triangular. A connected Lie group 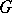is nilpotent if and only if in canonical coordinates (see Lie group) the group operation in 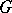is written polynomially [4]. Every simply-connected real nilpotent Lie group 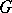is isomorphic to an algebraic group, and moreover, to an algebraic subgroup of .

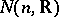A faithful representation of 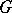in 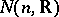can be chosen so that the automorphism group 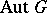can be imbedded in 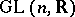as the normalizer of the image of 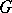(see [1]).

If 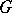is a connected matrix real nilpotent Lie group, then it splits into the direct product of a compact Abelian Lie group and a simply-connected Lie group. A connected linear algebraic group 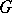over a field of characteristic 0 splits into the direct product of an Abelian normal subgroup consisting of the semi-simple elements and a normal subgroup consisting of the unipotent elements [5].

Nilpotent Lie groups were formerly called special Lie groups or Lie groups of rank 0. In the representation theory of semi-simple Lie groups, when studying discrete subgroups of such groups, substantial use was made of horospherical Lie groups that are nilpotent Lie groups.

References

[1]	G. Birkhoff, "Representability of Lie algebras and Lie groups by matrices" Ann. of Math. (2) , 38 (1937) pp. 526–532
[2]	N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)
[3]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French)
[4]	S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)
[5]	C. Chevalley, "Théorie des groupes de Lie" , 3 , Hermann (1955)

Comments

The theory of unitary representations of nilpotent Lie groups is well understood, and goes back to the fundamental paper [a1] of A.A. Kirillov. This theory, which is usually called the "orbit method" , has extensions to the case of solvable Lie groups, although the results are not as complete as in the nilpotent case. See also [a3].

References

[a1]	A.A. Kirillov, "Unitary representations of nilpotent Lie groups" Russian Math. Surveys , 17 : 4 (1962) pp. 53–104 Uspekhi Mat. Nauk , 17 : 4 (1962) pp. 57–110
[a2]	M.S. Raghunathan, "Discrete subgroups of Lie groups" , Springer (1972)
[a3]	L. Pukanszky, "Leçons sur les représentations des groupes" , Dunod (1967)