General-type algebraic surface
algebraic surface of general type
A surface of one of the broadest classes of algebraic surfaces (cf. Algebraic surface) in the Enriques classification. Namely, a smooth projective surface 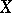 over an algebraically closed field
over an algebraically closed field 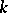 is called an algebraic surface of general type if
is called an algebraic surface of general type if
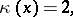 |
where 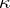 is the Kodaira dimension. This condition is equivalent to the fact that for an integer
is the Kodaira dimension. This condition is equivalent to the fact that for an integer 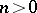 the linear system
the linear system 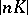 , where
, where 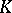 is the canonical divisor on
is the canonical divisor on  , defines a birational mapping of
, defines a birational mapping of 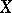 onto its image in
onto its image in 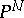 for a certain
for a certain 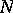 . Every algebraic surface of general type possesses a birational morphism onto its minimal model.
. Every algebraic surface of general type possesses a birational morphism onto its minimal model.
Minimal algebraic surfaces of general type are characterized (see [1], [3], [6]) by each of the following sets of properties:
a) 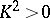 and
and 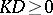 for any effective divisor
for any effective divisor 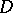 ;
;
b) 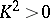 and
and 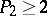 , where
, where 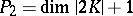 is the second plurigenus of
is the second plurigenus of 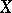 ;
;
c)  and the surface
and the surface 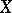 is not rational (cf. Rational surface);
is not rational (cf. Rational surface);
d) there exists an integer 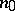 such that, for any
such that, for any 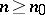 , the mapping
, the mapping 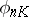 defined by the system
defined by the system 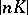 is a birational morphism of
is a birational morphism of 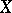 onto its image in
onto its image in 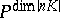 .
.
For algebraic surfaces of general type, relations (in the form of inequalities) exist between the numerical characteristics. Let 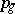 be the geometric genus and let
be the geometric genus and let 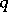 be the irregularity of
be the irregularity of 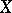 . Then for a minimal algebraic surface of general type the following inequalities hold:
. Then for a minimal algebraic surface of general type the following inequalities hold:
1) 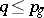 ;
;
2) 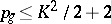 if
if 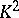 is even,
is even, 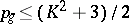 if
if 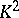 is odd (these two inequalities are called Noether's inequalities);
is odd (these two inequalities are called Noether's inequalities);
3) 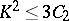 , where
, where 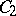 is the second Chern class of
is the second Chern class of 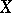 (or the topological Euler characteristic).
(or the topological Euler characteristic).
The most complete result on multi-canonical mappings 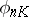 of algebraic surfaces of general type is the Bombieri–Kodaira theorem: Let
of algebraic surfaces of general type is the Bombieri–Kodaira theorem: Let 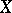 be a minimal algebraic surface of general type over an algebraically closed field of characteristic 0, then the mapping
be a minimal algebraic surface of general type over an algebraically closed field of characteristic 0, then the mapping
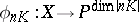 |
is a birational morphism onto its own image for all 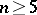 . Algebraic surfaces of general type for which
. Algebraic surfaces of general type for which 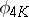 does not possess this property exist (see [5], , [9]).
does not possess this property exist (see [5], , [9]).
References
| [1] | I.R., et al. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) |
| [2] | F.A. Bogomolov, "Holomorphic tensors and vector bundles on projective varieties" Math. USSR-Izv. , 13 : 3 (1979) pp. 499–555 Izv. Akad. Nauk SSSR Ser. Mat. , 42 (1978) pp. 1227–1287 |
| [3] | A. Beauville, "Surfaces algébriques complexes" Astérisque , 54 (1978) |
| [4] | E. Bombieri, "Canonical models of surfaces of general type" Publ. Math. IHES , 42 (1972) pp. 447–495 |
| [5] | E. Bombieri, F. Catanese, "The tricanonical map of surfaces with 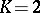 , , 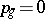 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 279–290 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 279–290 |
| [6] | D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1974) pp. 329–420 |
| [7] | E. Horikawa, "Algebraic surfaces of general type with small 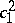 , I" Ann. of Math. , 104 (1976) pp. 357–387 , I" Ann. of Math. , 104 (1976) pp. 357–387 |
| [8a] | E. Horikawa, "Algebraic surfaces of general type with small 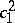 , II" Invent. Math. , 37 (1976) pp. 121–155 , II" Invent. Math. , 37 (1976) pp. 121–155 |
| [8b] | E. Horikawa, "Algebraic surfaces of general type with small 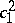 , III" Invent. Math. , 47 (1978) pp. 209–248 , III" Invent. Math. , 47 (1978) pp. 209–248 |
| [8c] | E. Horikawa, "Algebraic surfaces of general type with small 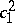 , IV" Invent. Math. , 50 (1978–1979) pp. 103–128 , IV" Invent. Math. , 50 (1978–1979) pp. 103–128 |
| [9] | K. Kodaira, "Pluricanonical systems on algebraic surfaces of general type" J. Math. Soc. Japan , 20 (1968) pp. 170–192 |
| [10] | Y. Miyaoka, "On the Chern numbers of surfaces of general type" Invent. Math. , 42 (1977) pp. 225–237 |
Comments
Some of the above results have only been proved in characteristic zero; for instance, the inequality 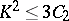 only holds in characteristic zero.
only holds in characteristic zero.
For results on canonical models of surfaces of general type in positive characteristic see [a2].
References
| [a1] | A. van de Ven, "Compact complex surfaces" , Springer (1984) |
| [a2] | T. Ekedahl, "Canonical models of surfaces of general type in positive characteristic" Publ. Math. IHES , 67 (1988) pp. 97–144 |
General-type algebraic surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=General-type_algebraic_surface&oldid=14784