Chern-Simons functional
A Lagrangian in the theory of gauge fields on an oriented manifold  of dimension
of dimension  . More precisely, it is a
. More precisely, it is a  -valued function
-valued function  on the space of connections ( "gauge fields" ) on a principal
on the space of connections ( "gauge fields" ) on a principal  -bundle (cf. also Principal
-bundle (cf. also Principal  -object) with base space
-object) with base space  for a compact connected Lie group
for a compact connected Lie group  . For
. For  simply connected, e.g.
simply connected, e.g.  , the bundle can be taken to be the product bundle and the Chern–Simons functional is given by the formula
, the bundle can be taken to be the product bundle and the Chern–Simons functional is given by the formula
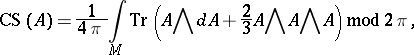 |
where the connection is given by the matrix-valued 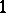 -form
-form  and
and 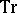 is the usual trace of matrices (cf. also Trace of a square matrix).
is the usual trace of matrices (cf. also Trace of a square matrix).
 is invariant under gauge transformations, i.e. automorphisms of the
is invariant under gauge transformations, i.e. automorphisms of the  -bundle, and hence it defines a Lagrangian on the space of orbits for the action of the group of these. The critical points of
-bundle, and hence it defines a Lagrangian on the space of orbits for the action of the group of these. The critical points of  are given by the flat connections, i.e. those for which the curvature
are given by the flat connections, i.e. those for which the curvature
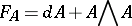 |
vanishes (cf. also Connection).
Applications of the Chern–Simons functional.
1) Using the Chern–Simons functional as a Morse function, A. Flöer [a6] defined invariants for homology  -spheres related to the Casson invariant (see [a7]).
-spheres related to the Casson invariant (see [a7]).
2) E. Witten [a8] used the Chern–Simons functional to set up a topological quantum field theory (cf. also Quantum field theory), which gives rise to invariants for knots and links in  -manifolds including the Jones polynomial for knots in the
-manifolds including the Jones polynomial for knots in the  -sphere. See also [a1] and [a2].
-sphere. See also [a1] and [a2].
The Chern–Simons functional is a special case of the Chern–Simons invariant and characteristic classes. General references are [a3], [a4], [a5].
References
| [a1] | S. Axelrod, I.M. Singer, "Chern–Simons perturbation theory" , Proc. XXth Internat. Conf. on Differential Geometric Methods in Theoretical Physics (New York, 1991) , World Sci. (1992) |
| [a2] | S. Axelrod, I.M. Singer, "Chern–Simons pertubation theory II" J. Diff. Geom. , 39 (1994) pp. 173–213 |
| [a3] | J. Cheeger, J. Simons, "Differential characters and geometric invariants" , Geometry and Topology (Maryland, 1983/4 , Lecture Notes Math. , 1167 , Springer (1985) |
| [a4] | S.-S. Chern, J. Simons, "Characteristic forms and geometric invariants" Ann. of Math. , 99 (1974) pp. 48–69 |
| [a5] | J.L. Dupont, F.W. Kamber, "On a generalization of Cheeger–Chern–Simons classes" Illinois J. Math. , 33 (1990) pp. 221–255 |
| [a6] | A. Floer, "An instanton-invariant for 3-manifolds" Comm. Math. Phys. , 118 (1988) pp. 215–240 |
| [a7] | C.H. Taubes, "Casson's invariant and gauge theory" J. Diff. Geom. , 31 (1990) pp. 547–599 |
| [a8] | E. Witten, "Quantum field theory and the Jones polynomial" Comm. Math. Phys. , 121 (1989) pp. 351–399 |
Chern-Simons functional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chern-Simons_functional&oldid=14746