Tamagawa measure
A measure  on the group
on the group  of adèles (cf. Adèle) of a connected linear algebraic group
of adèles (cf. Adèle) of a connected linear algebraic group 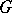 defined over a global field
defined over a global field 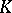 . This measure is constructed as follows: Let
. This measure is constructed as follows: Let 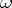 be a non-zero differential form on
be a non-zero differential form on 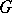 of maximum degree which is defined over
of maximum degree which is defined over 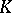 . For a valuation
. For a valuation  in the set
in the set 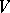 of equivalence classes of valuations of
of equivalence classes of valuations of 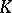 , one denotes by
, one denotes by 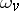 the Haar measure on the locally compact group
the Haar measure on the locally compact group 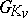 of points of
of points of 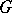 over the completion
over the completion 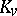 , obtained from
, obtained from 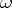 (see [1] and [2]). If the product
(see [1] and [2]). If the product 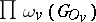 taken over all non-Archimedean
taken over all non-Archimedean  , where
, where 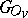 is the group of integral
is the group of integral  -adic points, is absolutely convergent (which is always the case for semi-simple and unipotent groups
-adic points, is absolutely convergent (which is always the case for semi-simple and unipotent groups 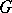 ), then one puts
), then one puts 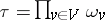 . (Otherwise, to define
. (Otherwise, to define  in some non-canonical way, one introduces a system of numbers
in some non-canonical way, one introduces a system of numbers 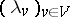 , called convergence factors, such that the product
, called convergence factors, such that the product 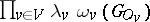 is absolutely convergent; then
is absolutely convergent; then  , see [1], [3].) The measure
, see [1], [3].) The measure  thus obtained does not depend on the initial choice of the form
thus obtained does not depend on the initial choice of the form 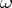 , and is the canonical Haar measure on
, and is the canonical Haar measure on  . This allows one to speak about the volume of homogeneous spaces connected with
. This allows one to speak about the volume of homogeneous spaces connected with 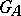 (see Tamagawa number).
(see Tamagawa number).
References
| [1] | A. Weil, "Sur certaines groupes d'opérateurs unitaires" Acta Math. , 111 (1964) pp. 143–211 |
| [2] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
| [3] | T. Ono, "On the Tamagawa number of algebraic tori" Ann. of Math. , 78 : 1 (1963) pp. 47–73 |
Comments
References
| [a1] | A. Weil, "Adèles and algebraic groups" , Birkhäuser (1982) |
Tamagawa measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tamagawa_measure&oldid=14742