Dirichlet distribution
From Encyclopedia of Mathematics
A probability distribution on the simplex
 |
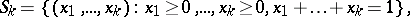where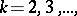 
determined by the probability density
 |
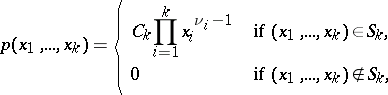where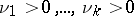 
and
 |
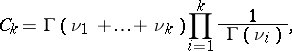where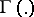 
is the gamma-function. If 
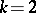, one has a special case of the Dirichlet distribution: the beta-distribution. The Dirichlet distribution plays an important role in the theory of order statistics. For instance, if 
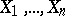are independent random variables that are uniformly distributed over the interval 
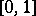and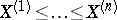 
are the corresponding order statistics (cf. Order statistic), the joint distribution of the 
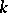differences
 |
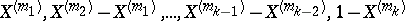(it is assumed that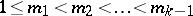 
) has the Dirichlet distribution with 
, 
, 
.
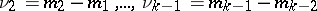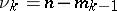References
| [1] | S.S. Wilks, "Mathematical statistics" , Wiley (1962) |
Comments
References
| [a1] | T.S. Ferguson, "A Bayesian analysis of some nonparametric problems" Ann. Stat. , 1 (1973) pp. 209–230 |
How to Cite This Entry:
Dirichlet distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_distribution&oldid=14736
Dirichlet distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirichlet_distribution&oldid=14736
This article was adapted from an original article by L.N. Bol'shev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article