Soft sheaf
A sheaf of sets 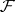 on a topological space
on a topological space 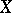 any section of which over some closed subset in
any section of which over some closed subset in  can be extended to a section of
can be extended to a section of 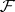 over all of
over all of 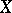 . Examples of soft sheaves are: the sheaf of germs of discontinuous sections of an arbitrary sheaf of sets on
. Examples of soft sheaves are: the sheaf of germs of discontinuous sections of an arbitrary sheaf of sets on 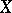 ; any flabby sheaf
; any flabby sheaf 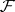 on a paracompact space
on a paracompact space 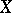 ; and any fine sheaf
; and any fine sheaf 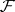 of Abelian groups on a paracompact space
of Abelian groups on a paracompact space 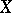 . The property of softness of a sheaf
. The property of softness of a sheaf 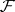 on a paracompact space
on a paracompact space 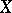 is local: A sheaf
is local: A sheaf 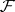 is soft if and only if any
is soft if and only if any 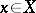 has an open neighbourhood
has an open neighbourhood 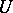 such that
such that 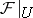 is a soft sheaf on
is a soft sheaf on 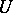 . A soft sheaf on a paracompact space induces a soft sheaf on any closed (and, if
. A soft sheaf on a paracompact space induces a soft sheaf on any closed (and, if 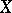 is metrizable, any locally closed) subspace. A sheaf of modules over a soft sheaf of rings is a soft sheaf.
is metrizable, any locally closed) subspace. A sheaf of modules over a soft sheaf of rings is a soft sheaf.
If
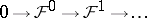 |
is an exact sequence of soft sheaves of Abelian groups on a paracompact space 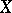 , then the corresponding sequence of groups of sections
, then the corresponding sequence of groups of sections
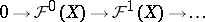 |
is also exact. The cohomology group  of any soft sheaf
of any soft sheaf 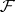 of Abelian groups on a paracompact space
of Abelian groups on a paracompact space 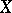 is trivial for
is trivial for 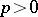 .
.
References
| [1] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) |
| [2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
Comments
References
| [a1] | G.E. Bredon, "Sheaf theory" , McGraw-Hill (1967) pp. §9 |
Soft sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Soft_sheaf&oldid=14711