Pesin theory
An important branch of the theory of dynamical systems (cf. Dynamical system) and of smooth ergodic theory, with many applications to non-linear dynamics. The name is due to the landmark work of Ya.B. Pesin in the mid-1970{}s [a20], [a21], [a22]. Sometimes Pesin theory is also referred to as the theory of smooth dynamical systems with non-uniformly hyperbolic behaviour, or simply the theory of non-uniformly hyperbolic dynamical systems.
Introduction.
One of the paradigms of dynamical systems is that the local instability of trajectories influences the global behaviour of the system, and paves the way to the existence of stochastic behaviour. Mathematically, instability of trajectories corresponds to some degree of hyperbolicity (cf. Hyperbolic set). The "strongest possible" kind of hyperbolicity occurs in the important class of Anosov systems (also called 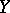 -systems, cf.
-systems, cf.  -system) [a1]. These are only known to occur in certain manifolds. Moreover, there are several results of topological nature showing that certain manifolds cannot carry Anosov systems.
-system) [a1]. These are only known to occur in certain manifolds. Moreover, there are several results of topological nature showing that certain manifolds cannot carry Anosov systems.
Pesin theory deals with a "weaker" kind of hyperbolicity, a much more common property that is believed to be "typical" : non-uniform hyperbolicity. Among the most important features due to hyperbolicity is the existence of invariant families of stable and unstable manifolds and their "absolute continuity" . The combination of hyperbolicity with non-trivial recurrence produces a rich and complicated orbit structure. The theory also describes the ergodic properties of smooth dynamical systems possessing an absolutely continuous invariant measure in terms of the Lyapunov exponents. One of the most striking consequences is the Pesin entropy formula, which expresses the metric entropy of the dynamical system in terms of its Lyapunov exponents.
Non-uniform hyperbolicity.
Let 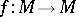 be a diffeomorphism of a compact manifold. It induces the discrete dynamical system (or cascade) composed of the powers
be a diffeomorphism of a compact manifold. It induces the discrete dynamical system (or cascade) composed of the powers 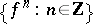 . Fix a Riemannian metric on
. Fix a Riemannian metric on 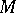 . The trajectory
. The trajectory 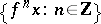 of a point
of a point 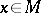 is called non-uniformly hyperbolic if there are positive numbers
is called non-uniformly hyperbolic if there are positive numbers 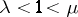 and splittings
and splittings 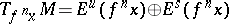 for each
for each 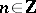 , and if for all sufficiently small
, and if for all sufficiently small 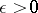 there is a positive function
there is a positive function 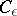 on the trajectory such that for every
on the trajectory such that for every 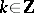 :
:
1) 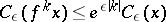 ;
;
2) 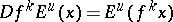 ,
, 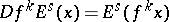 ;
;
3) if 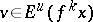 and
and 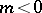 , then
, then
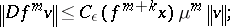 |
4) if  and
and 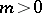 , then
, then
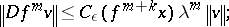 |
5) 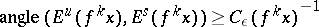 .
.
(The indices "s" and "u" refer, respectively, to "stable" and "unstable" .) The definition of non-uniformly partially hyperbolic trajectory is obtained by replacing the inequality 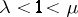 by the weaker requirement that
by the weaker requirement that 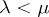 and
and 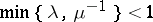 .
.
If 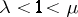 (respectively,
(respectively,  and
and  ) and the conditions 1)–5) hold for
) and the conditions 1)–5) hold for 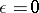 (i.e., if one can choose
(i.e., if one can choose 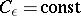 ), the trajectory is called uniformly hyperbolic (respectively, uniformly partially hyperbolic).
), the trajectory is called uniformly hyperbolic (respectively, uniformly partially hyperbolic).
The term "non-uniformly" means that the estimates in 3) and 4) may differ from the "uniform" estimates 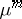 and
and 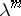 by at most slowly increasing terms along the trajectory, as in 1) (in the sense that the exponential rate
by at most slowly increasing terms along the trajectory, as in 1) (in the sense that the exponential rate  in 1) is small in comparison to the number
in 1) is small in comparison to the number 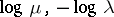 ); the term "partially" means that the hyperbolicity may hold only for a part of the tangent space.
); the term "partially" means that the hyperbolicity may hold only for a part of the tangent space.
One can similarly define the corresponding notions for a flow (continuous-time dynamical system) with 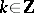 replaced by
replaced by 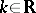 , and the splitting of the tangent spaces replaced by
, and the splitting of the tangent spaces replaced by 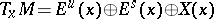 , where
, where 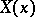 is the one-dimensional subspace generated by the flow direction.
is the one-dimensional subspace generated by the flow direction.
Stable and unstable manifolds.
Let  be a non-uniformly partially hyperbolic trajectory of a
be a non-uniformly partially hyperbolic trajectory of a 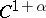 -diffeomorphism (
-diffeomorphism (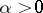 ). Assume that
). Assume that 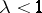 . Then there is a local stable manifold
. Then there is a local stable manifold 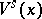 such that
such that 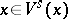 ,
, 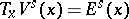 , and for every
, and for every 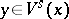 ,
, 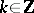 , and
, and 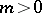 ,
,
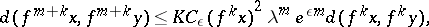 |
where 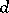 is the distance induced by the Riemannian metric and
is the distance induced by the Riemannian metric and  is a positive constant. The size
is a positive constant. The size 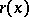 of
of  can be chosen in such a way that
can be chosen in such a way that 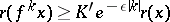 for every
for every 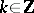 , where
, where 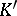 is a positive constant. If
is a positive constant. If 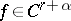 (
(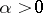 ), then
), then 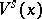 is of class
is of class 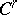 .
.
The global stable manifold of 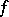 at
at  is defined by
is defined by 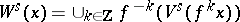 ; it is an immersed manifold with the same smoothness class as
; it is an immersed manifold with the same smoothness class as  . One has
. One has 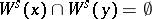 if
if 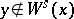 ,
, 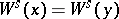 if
if 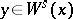 , and
, and 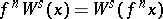 for every
for every 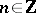 . The manifold
. The manifold 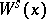 is independent of the particular size of the local stable manifolds
is independent of the particular size of the local stable manifolds 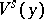 .
.
Similarly, when 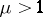 one can define a local (respectively, global) unstable manifold as a local (respectively, global) stable manifold of
one can define a local (respectively, global) unstable manifold as a local (respectively, global) stable manifold of 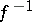 .
.
Non-uniformly hyperbolic dynamical systems and dynamical systems with non-zero Lyapunov exponents.
Let 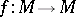 be a diffeomorphism and let
be a diffeomorphism and let  be a (finite) Borel
be a (finite) Borel 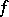 -invariant measure (cf. also Invariant measure). One calls
-invariant measure (cf. also Invariant measure). One calls 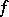 non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic) with respect to the measure
non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic) with respect to the measure  if the set
if the set 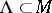 of points whose trajectories are non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic) is such that
of points whose trajectories are non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic) is such that 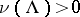 . In this case
. In this case 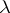 ,
, 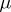 ,
,  , and
, and 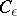 are replaced by measurable functions
are replaced by measurable functions 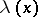 ,
, 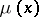 ,
, 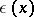 , and
, and 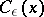 , respectively.
, respectively.
The set 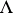 is
is 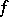 -invariant, i.e., it satisfies
-invariant, i.e., it satisfies 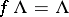 . Therefore, one can always assume that
. Therefore, one can always assume that 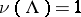 when
when 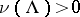 ; this means that if
; this means that if 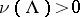 , then the measure
, then the measure 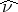 on
on 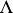 defined by
defined by 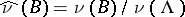 is
is 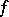 -invariant and
-invariant and 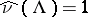 .
.
For 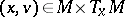 , one defines the forward upper Lyapunov exponent of
, one defines the forward upper Lyapunov exponent of 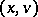 (with respect to
(with respect to 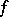 ) by
) by
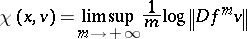 | (a1) |
for each 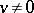 , and
, and  . For every
. For every 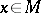 , there exist a positive integer
, there exist a positive integer 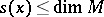 (the dimension of
(the dimension of  ) and collections of numbers
) and collections of numbers 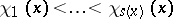 and linear subspaces
and linear subspaces 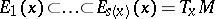 such that for every
such that for every  ,
,
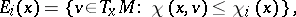 |
and if 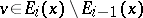 , then
, then 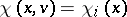 .
.
The numbers 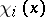 are called the values of the forward upper Lyapunov exponent at
are called the values of the forward upper Lyapunov exponent at  , and the collection of linear subspaces
, and the collection of linear subspaces 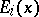 is called the forward filtration at
is called the forward filtration at  associated to
associated to 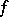 . The number
. The number 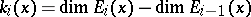 is the forward multiplicity of the exponent
is the forward multiplicity of the exponent 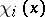 . One defines the forward spectrum of
. One defines the forward spectrum of 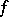 at
at  as the collection of pairs
as the collection of pairs 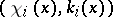 for
for 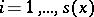 . Let
. Let 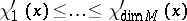 be the values of the forward upper Lyapunov exponent at
be the values of the forward upper Lyapunov exponent at  counted with multiplicities, i.e., in such a way that the exponent
counted with multiplicities, i.e., in such a way that the exponent 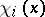 appears exactly a number
appears exactly a number  of times. The functions
of times. The functions 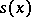 and
and 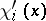 , for
, for 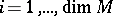 , are measurable and
, are measurable and 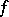 -invariant with respect to any
-invariant with respect to any 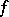 -invariant measure.
-invariant measure.
One defines the backward upper Lyapunov exponent of 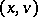 (with respect to
(with respect to 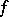 ) by an expression similar to (a1), with
) by an expression similar to (a1), with 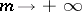 replaced by
replaced by 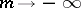 , and considers the corresponding backward spectrum.
, and considers the corresponding backward spectrum.
A Lyapunov-regular trajectory 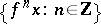 (see, for example, [a3], Sect. 2) is non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic) if and only if
(see, for example, [a3], Sect. 2) is non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic) if and only if 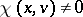 for all
for all 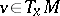 (respectively,
(respectively, 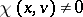 for some
for some 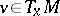 ). For flows, a Lyapunov-regular trajectory is non-uniformly hyperbolic if and only if
). For flows, a Lyapunov-regular trajectory is non-uniformly hyperbolic if and only if 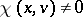 for all
for all 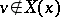 .
.
The multiplicative ergodic theorem of V. Oseledets [a19] implies that  -almost all points of
-almost all points of 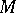 belong to a Lyapunov-regular trajectory. Therefore, for a given diffeomorphism, one has
belong to a Lyapunov-regular trajectory. Therefore, for a given diffeomorphism, one has  for all
for all 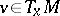 (respectively
(respectively 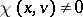 for some
for some 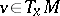 ) on a set of positive
) on a set of positive  -measure if and only if the diffeomorphism is non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic). Hence, the non-uniformly hyperbolic diffeomorphisms (with respect to the measure
-measure if and only if the diffeomorphism is non-uniformly hyperbolic (respectively, non-uniformly partially hyperbolic). Hence, the non-uniformly hyperbolic diffeomorphisms (with respect to the measure  ) are precisely the diffeomorphisms with non-zero Lyapunov exponents (on a set of positive
) are precisely the diffeomorphisms with non-zero Lyapunov exponents (on a set of positive  -measure).
-measure).
Furthermore, for  -almost every
-almost every 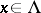 there exist subspaces
there exist subspaces  , for
, for  , such that for every
, such that for every 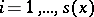 one has
one has  ,
,
 |
for every  , and if
, and if  , then
, then
 |
Pesin sets.
To a non-uniformly partially hyperbolic diffeomorphism one associates a filtration of measurable sets (not necessarily invariant) on which the estimates 3)–5) are uniform.
Let  be a non-uniformly hyperbolic diffeomorphism and let
be a non-uniformly hyperbolic diffeomorphism and let 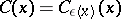 . Given
. Given 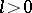 , one defines the measurable set
, one defines the measurable set  by
by
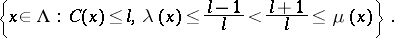 |
One has 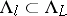 when
when 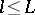 , and
, and 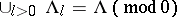 . Each set
. Each set 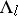 is closed but need not be
is closed but need not be 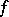 -invariant; for every
-invariant; for every 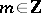 and
and 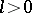 there exists an
there exists an  such that
such that 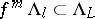 . The distribution
. The distribution 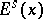 is, in general, only measurable on
is, in general, only measurable on 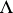 but it is continuous on
but it is continuous on 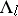 . The local stable manifolds
. The local stable manifolds 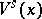 depend continuously on
depend continuously on 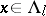 and their sizes are uniformly bounded below on
and their sizes are uniformly bounded below on 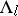 . Each set
. Each set 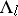 is called a Pesin set.
is called a Pesin set.
One similarly defines Pesin sets for arbitrary non-uniformly partially hyperbolic diffeomorphisms.
Lyapunov metrics and regular neighbourhoods.
Let 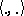 be the Riemannian metric on
be the Riemannian metric on 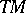 . For each fixed
. For each fixed 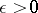 and every
and every 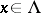 , one defines a Lyapunov metric on
, one defines a Lyapunov metric on 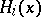 by
by
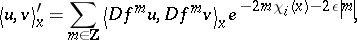 |
for each  . One extends this metric to
. One extends this metric to 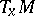 by declaring orthogonal the subspaces
by declaring orthogonal the subspaces 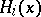 for
for 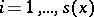 . The metric
. The metric 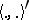 is continuous on
is continuous on 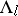 . The sequence of weights
. The sequence of weights 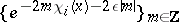 is called a Pesin tempering kernel. Any linear operator
is called a Pesin tempering kernel. Any linear operator 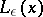 on
on 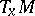 such that
such that
 |
is called a Lyapunov change of coordinates.
There exist a measurable function 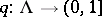 satisfying
satisfying 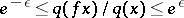 , and for each
, and for each 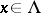 a collection of imbeddings
a collection of imbeddings 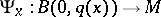 , defined on the ball
, defined on the ball 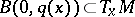 by
by 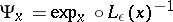 , such that if
, such that if  , then:
, then:
1) the derivative 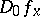 of
of 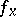 at the point
at the point  has the Lyapunov block form
has the Lyapunov block form
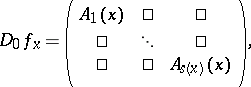 |
where each 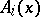 is an invertible linear operator between the
is an invertible linear operator between the 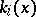 -dimensional spaces
-dimensional spaces  and
and 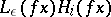 , for
, for 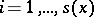 ;
;
2) for each 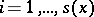 ,
,
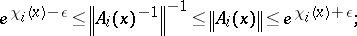 |
3) the 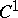 -distance between
-distance between 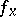 and
and 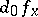 on the ball
on the ball 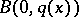 is at most
is at most  ;
;
4) there exist a constant 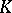 and a measurable function
and a measurable function 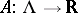 satisfying
satisfying 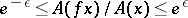 such that for every
such that for every 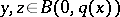 ,
,
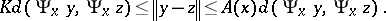 |
The function 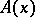 is bounded on each
is bounded on each 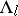 . The set
. The set 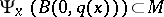 is called a regular neighbourhood of the point
is called a regular neighbourhood of the point  .
.
Absolute continuity.
A property playing a crucial role in the study of the ergodic properties of (uniformly and non-uniformly) hyperbolic dynamical systems is the absolute continuity of the families of stable and unstable manifolds. It allows one to pass from the local properties of the system to the study of its global behaviour.
Let  be an absolutely continuous
be an absolutely continuous 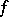 -invariant measure, i.e., an
-invariant measure, i.e., an 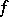 -invariant measure that is absolutely continuous with respect to Lebesgue measure (cf. Absolute continuity). For each
-invariant measure that is absolutely continuous with respect to Lebesgue measure (cf. Absolute continuity). For each 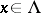 and
and 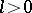 there exists a neighbourhood
there exists a neighbourhood 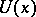 of
of  with size depending only on
with size depending only on 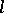 and with the following properties (see [a21]). Choose
and with the following properties (see [a21]). Choose 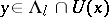 . Given two smooth manifolds
. Given two smooth manifolds  transversal to the local stable manifolds in
transversal to the local stable manifolds in 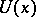 , one defines
, one defines
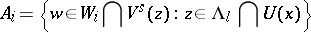 |
for 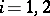 . Let
. Let  be the correspondence that takes
be the correspondence that takes 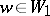 to the point
to the point 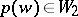 such that
such that 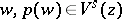 for some
for some  . If
. If 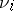 is the measure induced on
is the measure induced on 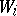 by the Riemannian metric, for
by the Riemannian metric, for 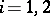 , then
, then  is absolutely continuous with respect to
is absolutely continuous with respect to 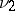 (if
(if 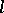 is sufficiently large, then
is sufficiently large, then 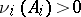 for
for 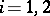 ).
).
This result has the following consequences (see [a21]). For each measurable set 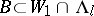 , let
, let 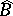 be the union of all the sets
be the union of all the sets 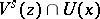 such that
such that 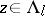 and
and 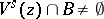 . The partition of
. The partition of  into the submanifolds
into the submanifolds 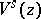 is a measurable partition (also called measurable decomposition), and the corresponding conditional measure of
is a measurable partition (also called measurable decomposition), and the corresponding conditional measure of  on
on 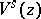 is absolutely continuous with respect to the measure
is absolutely continuous with respect to the measure 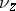 induced on
induced on  by the Riemannian metric, for each
by the Riemannian metric, for each 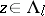 such that
such that 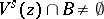 . In addition,
. In addition, 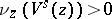 for
for  -almost all
-almost all 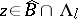 , and the measure
, and the measure 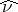 on
on 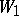 defined for each measurable set
defined for each measurable set  by
by 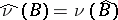 , is absolutely continuous with respect to
, is absolutely continuous with respect to 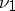 .
.
Smooth ergodic theory.
Let 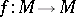 be a non-uniformly hyperbolic
be a non-uniformly hyperbolic 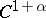 -diffeomorphism (
-diffeomorphism (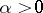 ) with respect to a Sinai–Ruelle–Bowen measure
) with respect to a Sinai–Ruelle–Bowen measure  , i.e., an
, i.e., an 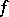 -invariant measure
-invariant measure  that has a non-zero Lyapunov exponent
that has a non-zero Lyapunov exponent  -almost everywhere and has absolutely continuous conditional measures on stable (or unstable) manifolds with respect to Lebesgue measure (in particular, this holds if
-almost everywhere and has absolutely continuous conditional measures on stable (or unstable) manifolds with respect to Lebesgue measure (in particular, this holds if  is absolutely continuous with respect to Lebesgue measure and has no zero Lyapunov exponents [a21]; see also above: "Absolute continuity" ). Then there is at most a countable number of disjoint
is absolutely continuous with respect to Lebesgue measure and has no zero Lyapunov exponents [a21]; see also above: "Absolute continuity" ). Then there is at most a countable number of disjoint 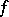 -invariant sets
-invariant sets 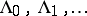 (the ergodic components) such that [a21], [a11]:
(the ergodic components) such that [a21], [a11]:
1) 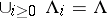 ,
, 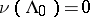 , and
, and 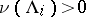 and
and 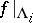 is ergodic (see Ergodicity) with respect to
is ergodic (see Ergodicity) with respect to 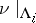 for every
for every 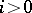 ;
;
2) each set 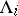 is a disjoint union of sets
is a disjoint union of sets 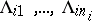 such that
such that  for each
for each 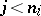 , and
, and 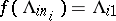 ;
;
3) for every 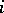 and
and 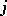 , there is a metric isomorphism between
, there is a metric isomorphism between 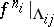 and a Bernoulli automorphism (in particular, the mapping
and a Bernoulli automorphism (in particular, the mapping 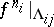 is a
is a 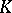 -system).
-system).
If  is an absolutely continuous
is an absolutely continuous  -invariant measure and the foliation
-invariant measure and the foliation 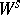 (or
(or  ) of
) of 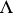 is
is 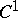 -continuous (i.e., for each
-continuous (i.e., for each 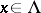 there is a neighbourhood of
there is a neighbourhood of  in
in 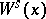 that is the image of an injective
that is the image of an injective 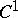 -mapping
-mapping 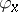 , defined on the ball with centre at
, defined on the ball with centre at  and of radius
and of radius 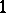 , and the mapping
, and the mapping 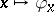 from
from 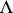 into the family of
into the family of 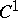 -mappings is continuous), then any ergodic component of positive
-mappings is continuous), then any ergodic component of positive  -measure is an open set (mod
-measure is an open set (mod  ); if, in addition,
); if, in addition, 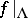 is topologically transitive (cf. Topological transitivity; Chaos), then
is topologically transitive (cf. Topological transitivity; Chaos), then 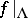 is ergodic [a21].
is ergodic [a21].
If 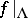 is ergodic, then for Lebesgue-almost-every point
is ergodic, then for Lebesgue-almost-every point 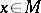 and every continuous function
and every continuous function 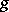 , one has
, one has
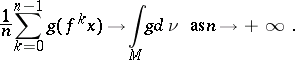 |
There is a measurable partition 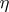 of
of 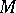 with the following properties:
with the following properties:
1) for  -almost every
-almost every 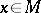 , the element
, the element 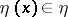 containing
containing  is an open subset (mod
is an open subset (mod  ) of
) of 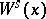 ;
;
2) 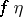 is a refinement of
is a refinement of 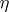 , and
, and 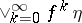 is the partition of
is the partition of 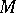 into points;
into points;
3) 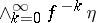 coincides with the measurable hull of
coincides with the measurable hull of 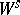 , as well as with the maximal partition with zero entropy (the
, as well as with the maximal partition with zero entropy (the 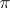 -partition for
-partition for 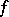 ; see Entropy of a measurable decomposition);
; see Entropy of a measurable decomposition);
4) 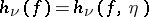 (cf. Entropy theory of a dynamical system).
(cf. Entropy theory of a dynamical system).
Pesin entropy formula.
For a 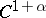 -diffeomorphism (
-diffeomorphism (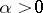 )
)  of a compact manifold and an absolutely continuous
of a compact manifold and an absolutely continuous 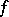 -invariant probability measure
-invariant probability measure  , the metric entropy
, the metric entropy 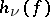 of
of 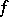 with respect to
with respect to  is given by the Pesin entropy formula [a21]
is given by the Pesin entropy formula [a21]
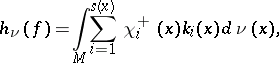 | (a2) |
where 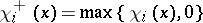 and
and 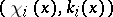 form the forward spectrum of
form the forward spectrum of 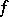 at
at  .
.
For a 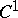 -diffeomorphism
-diffeomorphism  of a compact manifold and an
of a compact manifold and an 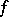 -invariant probability measure
-invariant probability measure  , the Ruelle inequality holds [a25]:
, the Ruelle inequality holds [a25]:
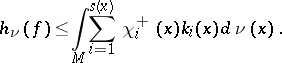 | (a3) |
An important consequence of (a3) is that any  -diffeomorphism with positive topological entropy has an
-diffeomorphism with positive topological entropy has an 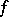 -invariant measure with at least one positive and one negative Lyapunov exponent; in particular, for surface diffeomorphisms there is an
-invariant measure with at least one positive and one negative Lyapunov exponent; in particular, for surface diffeomorphisms there is an 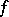 -invariant measure with every exponent non-zero. For arbitrary invariant measures the inequality (a3) may be strict [a7].
-invariant measure with every exponent non-zero. For arbitrary invariant measures the inequality (a3) may be strict [a7].
The formula (a2) was first established by Pesin in [a21]. A proof which does not use the theory of invariant manifolds and absolute continuity was given by R. Mañé [a17]. For 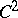 -diffeomorphisms, (a2) holds if and only if
-diffeomorphisms, (a2) holds if and only if  has absolutely continuous conditional measures on unstable manifolds [a13], [a12].
has absolutely continuous conditional measures on unstable manifolds [a13], [a12].
The formula (a2) has been extended to mappings with singularities [a12]. For 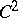 -diffeomorphisms and arbitrary invariant measures, results of F. Ledrappier and L.-S. Young [a14] show that the possible defect between the left- and right-hand sides of (a3) is due to the defects between
-diffeomorphisms and arbitrary invariant measures, results of F. Ledrappier and L.-S. Young [a14] show that the possible defect between the left- and right-hand sides of (a3) is due to the defects between 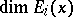 and the Hausdorff dimension of
and the Hausdorff dimension of  "in the direction of Eix" for each
"in the direction of Eix" for each 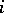 .
.
Hyperbolic measures.
Let 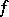 be a
be a 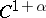 -diffeomorphism (
-diffeomorphism (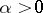 ) and let
) and let  be an
be an 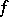 -invariant measure. One says that
-invariant measure. One says that  is hyperbolic (with respect to
is hyperbolic (with respect to 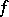 ) if
) if 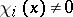 for
for  -almost every
-almost every 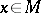 and all
and all 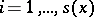 . The measure
. The measure  is hyperbolic (with respect to
is hyperbolic (with respect to 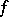 ) if and only if
) if and only if 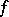 is non-uniformly hyperbolic with respect to
is non-uniformly hyperbolic with respect to  (and the set
(and the set 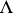 has full
has full  -measure). The fundamental work of A. Katok has revealed a rich and complicated orbit structure for diffeomorphisms possessing a hyperbolic measure.
-measure). The fundamental work of A. Katok has revealed a rich and complicated orbit structure for diffeomorphisms possessing a hyperbolic measure.
Let  be a hyperbolic measure. The support of
be a hyperbolic measure. The support of  is contained in the closure of the set of periodic points. If
is contained in the closure of the set of periodic points. If  is ergodic and not concentrated on a periodic orbit, then [a7], [a9]:
is ergodic and not concentrated on a periodic orbit, then [a7], [a9]:
1) the support of  is contained in the closure of the set of hyperbolic periodic points possessing a transversal homoclinic point;
is contained in the closure of the set of hyperbolic periodic points possessing a transversal homoclinic point;
2) for every 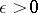 there exists a closed
there exists a closed 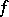 -invariant hyperbolic set
-invariant hyperbolic set 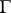 such that the restriction of
such that the restriction of 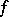 to
to 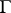 is topologically conjugate to a topological Markov chain with topological entropy
is topologically conjugate to a topological Markov chain with topological entropy 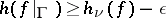 , i.e., the entropy of a hyperbolic measure can be approximated by the topological entropies of invariant hyperbolic sets.
, i.e., the entropy of a hyperbolic measure can be approximated by the topological entropies of invariant hyperbolic sets.
If 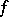 possesses a hyperbolic measure, then
possesses a hyperbolic measure, then 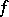 satisfies a closing lemma: given
satisfies a closing lemma: given  , there exists a
, there exists a 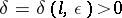 such that for each
such that for each 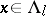 and each integer
and each integer  satisfying
satisfying 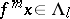 and
and 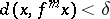 , there exists a point
, there exists a point  such that
such that 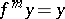 ,
, 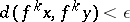 for every
for every 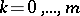 , and
, and 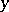 is a hyperbolic periodic point [a7]. The diffeomorphism
is a hyperbolic periodic point [a7]. The diffeomorphism 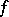 also satisfies a shadowing lemma (see [a9]) and a Lifschitz-type theorem [a9]: if
also satisfies a shadowing lemma (see [a9]) and a Lifschitz-type theorem [a9]: if 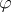 is a Hölder-continuous function (cf. Hölder condition) such that
is a Hölder-continuous function (cf. Hölder condition) such that 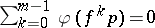 for each periodic point
for each periodic point 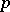 with
with  , then there is a measurable function
, then there is a measurable function 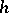 such that
such that 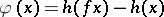 for
for  -almost every
-almost every  .
.
Let 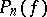 be the number of periodic points of
be the number of periodic points of 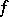 with period
with period  . If
. If 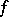 possesses a hyperbolic measure or is a surface diffeomorphism, then
possesses a hyperbolic measure or is a surface diffeomorphism, then
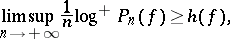 |
where 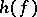 is the topological entropy of
is the topological entropy of 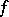 [a7].
[a7].
Let  be a hyperbolic ergodic measure. L.M. Barreira, Pesin and J. Schmeling [a2] have shown that there is a constant
be a hyperbolic ergodic measure. L.M. Barreira, Pesin and J. Schmeling [a2] have shown that there is a constant 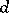 such that for
such that for  -almost every
-almost every 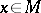 ,
,
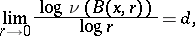 |
where 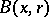 is the ball in
is the ball in 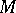 with centre at
with centre at  and of radius
and of radius  (this claim was known as the Eckmann–Ruelle conjecture); this implies that the Hausdorff dimension of
(this claim was known as the Eckmann–Ruelle conjecture); this implies that the Hausdorff dimension of  and the lower and upper box dimensions of
and the lower and upper box dimensions of  coincide and are equal to
coincide and are equal to  (see [a2]). Ledrappier and Young [a14] have shown that if
(see [a2]). Ledrappier and Young [a14] have shown that if  (respectively,
(respectively, 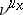 ) are the conditional measures of
) are the conditional measures of  with respect to the stable (respectively, unstable) manifolds, then there are constants
with respect to the stable (respectively, unstable) manifolds, then there are constants 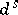 and
and 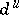 such that for
such that for  -almost every
-almost every 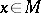 ,
,
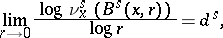 |
 |
where 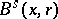 (respectively,
(respectively, 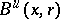 ) is the ball in
) is the ball in 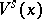 (respectively,
(respectively, 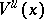 ) with centre at
) with centre at  and of radius
and of radius  . Moreover,
. Moreover, 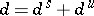 [a2] and
[a2] and  has an "almost product structure" (see [a2]).
has an "almost product structure" (see [a2]).
Criteria for having non-zero Lyapunov exponents.
Above it has been shown that non-uniformly hyperbolic dynamical systems possess strong ergodic properties, as well as many other important properties. Therefore, it is of primary interest to have verifiable methods for checking the non-vanishing of Lyapunov exponents.
The following Katok–Burns criterion holds: A real-valued measurable function 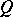 on the tangent bundle
on the tangent bundle 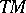 is called an eventually strict Lyapunov function if for
is called an eventually strict Lyapunov function if for  -almost every
-almost every 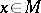 :
:
1) the function 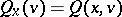 is continuous, homogeneous of degree one and takes both positive and negative values;
is continuous, homogeneous of degree one and takes both positive and negative values;
2) the maximal dimensions of the linear subspaces contained, respectively, in the sets 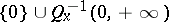 and
and 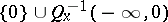 are constants
are constants 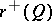 and
and 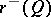 , and
, and 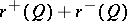 is the dimension of
is the dimension of  ;
;
3) 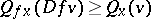 for all
for all  ;
;
4) there exists a positive integer 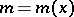 such that for all
such that for all  ,
,
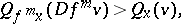 |
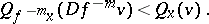 |
If 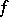 possesses an eventually strict Lyapunov function, then there exist exactly
possesses an eventually strict Lyapunov function, then there exist exactly 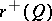 positive Lyapunov exponents and
positive Lyapunov exponents and 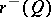 negative ones [a8] (see also [a28]).
negative ones [a8] (see also [a28]).
Another method to estimate the Lyapunov exponents was presented in [a6].
Generalizations.
There are several natural and important generalizations of Pesin theory. Examples of these are: generalizations to non-invertible mappings; extensions of the main results of Pesin's work to mappings with singularities [a10], including billiard systems and other physical models; infinite-dimensional versions of results on stable and unstable manifolds in Hilbert spaces [a27] and Banach spaces [a18], given certain compactness assumptions; some results have been extended to random mappings [a15].
Related results have been obtained for products of random matrices (see [a5] and the references therein).
References
| [a1] | D. Anosov, "Geodesic flows on closed Riemann manifolds with negative curvature" Proc. Steklov Inst. Math. , 90 (1969) (In Russian) |
| [a2] | L. Barreira, Ya. Pesin, J. Schmeling, "On the pointwise dimension of hyperbolic measures: A proof of the Eckmann–Ruelle conjecture" Electronic Research Announc. Amer. Math. Soc. , 2 (1996) |
| [a3] | I. Cornfeld, Ya. Sinai, "Basic notions of ergodic theory and examples of dynamical systems" Ya. Sinai (ed.) , Dynamical Systems II , Encycl. Math. Sci. , 2 , Springer (1989) pp. 2–27 (In Russian) |
| [a4] | A. Fathi, M. Herman, J. Yoccoz, "A proof of Pesin's stable manifold theorem" J. Palis (ed.) , Geometric Dynamics , Lecture Notes in Mathematics , 1007 , Springer (1983) pp. 177–215 |
| [a5] | I. Goldsheid, G. Margulis, "Lyapunov exponents of a product of random matrices" Russian Math. Surveys , 44 (1989) pp. 11–71 (In Russian) |
| [a6] | M. Herman, "Une méthode pour minorer les exposants de Lyapunov et quelques examples montrant le caractére local d'un théorèm d'Arnold et de Moser sur le tore de dimension  " Comment. Math. Helv. , 58 (1983) pp. 453–502 " Comment. Math. Helv. , 58 (1983) pp. 453–502 |
| [a7] | A. Katok, "Lyapunov exponents, entropy and periodic orbits for diffeomorphisms" IHES Publ. Math. , 51 (1980) pp. 137–173 |
| [a8] | A. Katok, K. Burns, "Infinitesimal Lyapunov functions, invariant cone families and stochastic properties of smooth dynamical systems" Ergodic Th. Dynamical Systems , 14 (1994) pp. 757–785 |
| [a9] | A. Katok, L. Mendoza, "Dynamical systems with nonuniformly hyperbolic behavior" A. Katok (ed.) B. Hasselblatt (ed.) , Introduction to the Modern Theory of Dynamical Systems , Cambridge Univ. Press (1995) |
| [a10] | A. Katok, J.-M. Strelcyn, "Invariant manifolds, entropy and billiards; smooth maps with singularities" , Lecture Notes in Mathematics , 1222 , Springer (1986) (with the collaboration of F. Ledrappier and F. Przytycki) |
| [a11] | F. Ledrappier, "Propriétés ergodiques des mesures de Sinaï" IHES Publ. Math. , 59 (1984) pp. 163–188 |
| [a12] | F. Ledrappier, J.-M. Strelcyn, "A proof of the estimate from below in Pesin's entropy formula" Ergodic Th. Dynamical Systems , 2 (1982) pp. 203–219 |
| [a13] | F. Ledrappier, L.-S. Young, "The metric entropy of diffeomorphisms I. Characterization of measures satisfying Pesin's entropy formula" Ann. of Math. (2) , 122 (1985) pp. 509–539 |
| [a14] | F. Ledrappier, L.-S. Young, "The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension" Ann. of Math. (2) , 122 (1985) pp. 540–574 |
| [a15] | P.-D. Liu, M. Qian, "Smooth ergodic theory of random dynamical systems" , Lecture Notes in Mathematics , 1606 , Springer (1995) |
| [a16] | C. Liverani, M. Wojtkowski, "Ergodicity in Hamiltonian systems" , Dynamics Reported Expositions in Dynamical Systems (N.S.) , 4 , Springer (1995) pp. 130–202 |
| [a17] | R. Mané, "A proof of Pesin's formula" Ergodic Th. Dynamical Systems , 1 (1981) pp. 95–102 (Errata: 3 (1983), 159–160) |
| [a18] | R. Mané, "Lyapunov exponents and stable manifolds for compact transformations" J. Palis (ed.) , Geometric Dynamics , Lecture Notes in Mathematics , 1007 , Springer (1983) pp. 522–577 |
| [a19] | V. Oseledets, "A multiplicative ergodic theorem. Liapunov characteristic numbers for dynamical systems" Trans. Moscow Math. Soc. , 19 (1968) pp. 197–221 (In Russian) |
| [a20] | Ya. Pesin, "Families of invariant manifolds corresponding to nonzero characteristic exponents" Math. USSR Izv. , 10 (1976) pp. 1261–1305 (In Russian) |
| [a21] | Ya. Pesin, "Characteristic exponents and smooth ergodic theory" Russian Math. Surveys , 32 (1977) pp. 55–114 (In Russian) |
| [a22] | Ya. Pesin, "Geodesic flows on closed Riemannian manifolds without focal points" Math. USSR Izv. , 11 (1977) pp. 1195–1228 (In Russian) |
| [a23] | Ya. Pesin, "General theory of smooth hyperbolic dynamical systems" Ya. Sinai (ed.) , Dynamical Systems II , Encycl. Math. Sci. , 2 , Springer (1989) pp. 108–151 (In Russian) |
| [a24] | C. Pugh, M. Shub, "Ergodic attractors" Trans. Amer. Math. Soc. , 312 (1989) pp. 1–54 |
| [a25] | D. Ruelle, "An inequality for the entropy of differentiable maps" Bol. Soc. Brasil. Mat. , 9 (1978) pp. 83–87 |
| [a26] | D. Ruelle, "Ergodic theory of differentiable dynamical systems" IHES Publ. Math. , 50 (1979) pp. 27–58 |
| [a27] | D. Ruelle, "Characteristic exponents and invariant manifolds in Hilbert space" Ann. of Math. (2) , 115 (1982) pp. 243–290 |
| [a28] | M. Wojtkowski, "Invariant families of cones and Lyapunov exponents" Ergodic Th. Dynamical Systems , 5 (1985) pp. 145–161 |
Pesin theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pesin_theory&oldid=14695