Moreau envelope function
Moreau envelope
Let 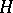 be a real Hilbert space and let
be a real Hilbert space and let 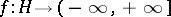 be a lower semi-continuous extended-real-valued function (cf. also Continuous function) such that for a certain
be a lower semi-continuous extended-real-valued function (cf. also Continuous function) such that for a certain  ,
,
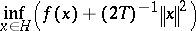 |
is finite. For 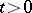 , the Moreau envelope function
, the Moreau envelope function  is defined by infimal convolution of
is defined by infimal convolution of 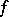 with
with 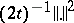 , i.e.,
, i.e.,
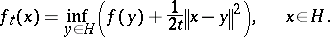 | (a1) |
This operation amounts geometrically to performing vector addition of the strict epigraphs of  and
and  . The Moreau envelopes are usually utilized as approximants of
. The Moreau envelopes are usually utilized as approximants of  , although regularization was not the purpose of the seminal paper [a12].
, although regularization was not the purpose of the seminal paper [a12].
If  ,
, 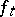 is everywhere finite and Lipschitz continuous (cf. also Lipschitz condition) on bounded sets. Moreover,
is everywhere finite and Lipschitz continuous (cf. also Lipschitz condition) on bounded sets. Moreover, 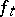 increases pointwise to
increases pointwise to  as
as 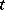 decreases to
decreases to  ; the convergence is in fact uniform on bounded sets (cf. also Uniform convergence) when
; the convergence is in fact uniform on bounded sets (cf. also Uniform convergence) when  is uniformly continuous on bounded sets (cf. also Uniform continuity). One might expect that under some additional assumptions on
is uniformly continuous on bounded sets (cf. also Uniform continuity). One might expect that under some additional assumptions on  the differentiability properties of the square of the norm in
the differentiability properties of the square of the norm in 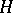 should to some extent carry over to
should to some extent carry over to 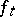 , thus giving rise to a smooth regularization of
, thus giving rise to a smooth regularization of 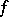 . This is true in the presence of convexity.
. This is true in the presence of convexity.
The convex case.
Suppose  is convex (cf. also Convex function (of a real variable)). Then
is convex (cf. also Convex function (of a real variable)). Then 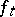 is differentiable and
is differentiable and 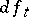 is globally Lipschitz continuous of rate
is globally Lipschitz continuous of rate 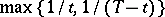 when
when 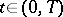 . Furthermore,
. Furthermore, 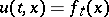 is a classical solution of
is a classical solution of
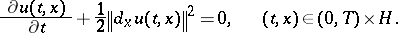 |
Let the subdifferential of  be defined by
be defined by
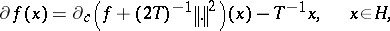 |
where the first term at the right-hand side is the subdifferential in the sense of convex analysis of the convex function 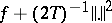 (
(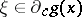 means that
means that  is finite and
is finite and 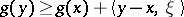 for all
for all 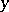 ). The infimum (a1) is achieved at a unique point
). The infimum (a1) is achieved at a unique point 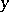 , which is denoted by
, which is denoted by 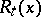 and is given by
and is given by 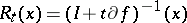 . Furthermore,
. Furthermore,
 |
which justifies the alternative term Moreau–Yosida approximation, since 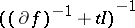 ,
, 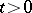 , are the Yosida approximants of
, are the Yosida approximants of 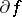 . Moreover,
. Moreover,  in the sense of Kuratowski–Painlevé convergence of graphs in
in the sense of Kuratowski–Painlevé convergence of graphs in 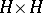 , while
, while 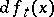 converges to the element of
converges to the element of 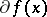 of minimal norm unless
of minimal norm unless  is empty. Stationary points and values are preserved; as a matter of fact, if
is empty. Stationary points and values are preserved; as a matter of fact, if 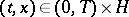 , then
, then
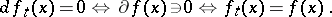 |
For various applications and further properties, consult [a3], [a4], [a1], [a2].
Regularization in the non-convex case.
If one insists on a smooth regularization, the Moreau envelopes cannot be used for arbitrary functions. This is however not a serious drawback. It is easy to see that 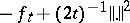 is always a convex function, so that
is always a convex function, so that 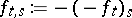 is smooth when
is smooth when 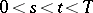 ; in fact,
; in fact, 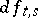 is globally Lipschitz continuous of rate
is globally Lipschitz continuous of rate 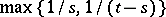 . Explicitly,
. Explicitly,
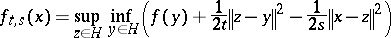 |
for all  .
.
Moreover, 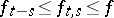 and hence
and hence 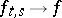 pointwise as
pointwise as 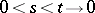 . The double envelopes
. The double envelopes 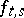 , frequently called the Lasry–Lions approximants of
, frequently called the Lasry–Lions approximants of 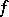 , were introduced and investigated by J.-M. Lasry and P.-L. Lions in [a10]; see also [a4], [a13]. One can prove that the equation
, were introduced and investigated by J.-M. Lasry and P.-L. Lions in [a10]; see also [a4], [a13]. One can prove that the equation 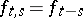 is true for all
is true for all 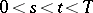 exactly when
exactly when 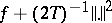 is a convex function [a13], in which case therefore the approximation method reduces to the previous one.
is a convex function [a13], in which case therefore the approximation method reduces to the previous one.
Connections with the Hamilton–Jacobi equation.
As stated above, 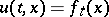 furnishes a classical solution of the initial-value problem
furnishes a classical solution of the initial-value problem
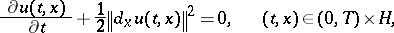 |
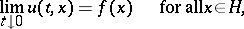 |
if 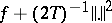 is a convex function. Let, now,
is a convex function. Let, now, 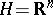 and drop the convexity hypothesis on
and drop the convexity hypothesis on  . While being non-differentiable in general,
. While being non-differentiable in general, 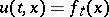 is nonetheless locally Lipschitz continuous in
is nonetheless locally Lipschitz continuous in 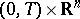 and is known to be the unique viscosity solution of the above initial-value problem [a11], [a14]. (This notion of a generalized solution allows merely continuous functions to be solutions, [a6]; cf. Viscosity solutions). In this context, (a1) is referred to as the Lax formula; the Lax formula is intimately related to the Hopf formula for conservation laws, see [a9], [a7], [a8], [a11].
and is known to be the unique viscosity solution of the above initial-value problem [a11], [a14]. (This notion of a generalized solution allows merely continuous functions to be solutions, [a6]; cf. Viscosity solutions). In this context, (a1) is referred to as the Lax formula; the Lax formula is intimately related to the Hopf formula for conservation laws, see [a9], [a7], [a8], [a11].
Extensions to Banach spaces.
The Lasry–Lions regularization scheme has been extended to certain classes of Banach spaces 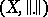 . For the case where
. For the case where  and the dual norm
and the dual norm 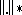 are simultaneously locally uniformly rotund, an approach by means of the Legendre–Fenchel transformation has been taken in [a13]. Another extension appears in [a5], under the hypothesis that
are simultaneously locally uniformly rotund, an approach by means of the Legendre–Fenchel transformation has been taken in [a13]. Another extension appears in [a5], under the hypothesis that  be super-reflexive (cf. also Reflexive space).
be super-reflexive (cf. also Reflexive space).
For more on the theme of regularization, see (the editorial comments to) Regularization and Regularization method.
References
| [a1] | I. Ekeland, J.M. Lasry, "On the number of periodic trajectories for a Hamiltonian flow on a convex energy surface" Ann. of Math. , 112 (1980) pp. 283–319 |
| [a2] | R.T. Rockafellar, R.J.-B. Wets, "Variational analysis" , Springer (1998) |
| [a3] | H. Attouch, "Variational convergence for functions and operators" , Applicable Math. , Pitman (1984) |
| [a4] | H. Attouch, D. Azé, "Approximation and regularization of arbitrary functions in Hilbert spaces by the Lasry–Lions method" Ann. Inst. H. Poincaré Anal. Non Lin. , 10 (1993) pp. 289–312 |
| [a5] | M. Cepedello–Boiso, "On regularization in superreflexive Banach spaces by infimal convolution formulas" Studia Math. , 129 (1998) pp. 265–284 |
| [a6] | M.G. Crandall, P.-L. Lions, "Viscosity solutions of Hamilton–Jacobi equations" Trans. Amer. Math. Soc. , 277 (1983) pp. 1–42 |
| [a7] | E. Hopf, "The partial differential equation 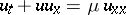 " Commun. Pure Appl. Math. , 3 (1950) pp. 201–230 " Commun. Pure Appl. Math. , 3 (1950) pp. 201–230 |
| [a8] | E. Hopf, "Generalized solutions of non-linear equations of first order" J. Math. Mech. , 14 (1965) pp. 951–973 |
| [a9] | P.D. Lax, "Hyperbolic systems of conservation laws II" Commun. Pure Appl. Math. , 10 (1957) pp. 537–566 |
| [a10] | J.-M. Lasry, P.-L. Lions, "A remark on regularization in Hilbert spaces" Israel J. Math. , 55 (1986) pp. 257–266 |
| [a11] | P.-L. Lions, "Generalized solutions of Hamilton–Jacobi equations" , Res. Notes Math. , 69 , Pitman (1982) |
| [a12] | J-J. Moreau, "Proximité et dualité dans un espace hilbertien" Bull. Soc. Math. France , 93 (1965) pp. 273–299 |
| [a13] | T. Strömberg, "On regularization in Banach spaces" Ark. Mat. , 34 (1996) pp. 383–406 |
| [a14] | T. Strömberg, "Hopf's formula gives the unique viscosity solution" Math. Scand. (submitted) |
Moreau envelope function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Moreau_envelope_function&oldid=14680