Normal bundle

of a submanifold

The vector bundle consisting of tangent vectors to the ambient manifold that are normal to the submanifold. If is a Riemannian manifold, is an (immersed) submanifold of it, and are the tangent bundles over and (cf. Tangent bundle), then the normal bundle of is the subbundle in consisting of the vectors 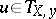, , 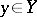that are orthogonal to .

With the help of normal bundles one constructs, for example, tubular neighbourhoods of submanifolds (cf. Tubular neighbourhood). The normal bundle over 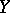, regarded up to equivalence, does not depend on the choice of the Riemannian metric on 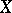, since it can be defined without recourse to the metric as the quotient bundle 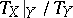of the tangent bundle 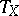restricted to 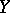by the vector bundle 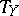. Somewhat more general is the construction of the normal bundle of an arbitrary immersion (cf. Immersion of a manifold) 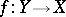of differentiable manifolds:

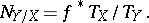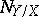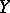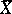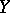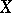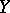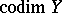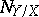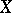Similarly one defines the normal bundle of a non-singular algebraic subvariety in a non-singular algebraic variety or that of an analytic submanifold in an analytic manifold ; it is an algebraic (or analytic) vector bundle over of rank . In particular, if , then is isomorphic to the restriction to of the bundle over that determines the divisor .

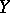When 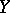is an analytic subspace of an analytic space 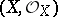, the normal bundle of is sometimes defined as the analytic family of vector spaces dual to the conormal sheaf 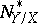(see Normal sheaf). For applications of normal bundles to the problem of contractibility of submanifolds see Exceptional analytic set; Exceptional subvariety.

References

[1]	A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" J. Soviet Math. , 14 : 3 (1980) pp. 1363–1406 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 15 (1977) pp. 93–156
[2]	J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974)
[3]	V.A. Rokhlin, D.B. Fuks, "Beginner's course in topology. Geometric chapters" , Springer (1984) (Translated from Russian)
[4]	M.W. Hirsch, "Differential topology" , Springer (1976)
[5]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)

References

[a1]	N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951)