Subdifferential
of a convex function 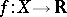 at a point
at a point 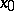 , defined on a space
, defined on a space 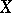 that is in duality with a space
that is in duality with a space 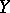
The set in 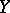 defined by:
defined by:
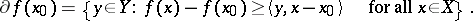 |
For example, the subdifferential of the norm 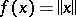 in a normed space
in a normed space 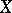 with dual space
with dual space 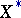 takes the form
takes the form
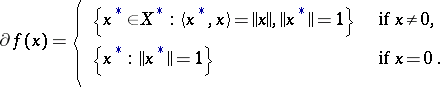 |
The subdifferential of a convex function 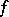 at a point
at a point 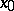 is a convex set. If
is a convex set. If 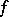 is continuous at this point, then the subdifferential is non-empty and compact in the topology
is continuous at this point, then the subdifferential is non-empty and compact in the topology 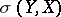 .
.
The role of the subdifferential of a convex function is similar to that of the derivative in classical analysis. Theorems for subdifferentials that are analogous to theorems for derivatives are valid. For example, if 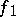 and
and 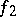 are convex functions and if, at a point
are convex functions and if, at a point 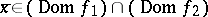 , at least one of the functions is continuous, then
, at least one of the functions is continuous, then
 |
for all  (the Moreau–Rockafellar theorem).
(the Moreau–Rockafellar theorem).
The subdifferential of the support function of a convex set 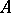 in
in 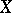 that is compact in the topology
that is compact in the topology 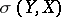 coincides with the set
coincides with the set 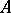 itself. This expresses the duality between convex compact sets and convex closed homogeneous functions (see also Support function; Supergraph; Convex analysis).
itself. This expresses the duality between convex compact sets and convex closed homogeneous functions (see also Support function; Supergraph; Convex analysis).
References
| [1] | R.T. Rockafellar, "Convex analysis" , Princeton Univ. Press (1970) |
Comments
The 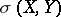 -topology is the weak topology on
-topology is the weak topology on  defined by the family of semi-norms
defined by the family of semi-norms 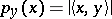 ,
, 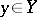 ; this is the weakest topology which makes all the functionals
; this is the weakest topology which makes all the functionals 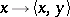 continuous.
continuous.
The elements 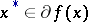 are called subgradients of
are called subgradients of 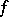 at
at  .
.
References
| [a1] | R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 13–59 |
| [a2] | V. Barbu, Th. Precupanu, "Convexity and optimization in Banach spaces" , Reidel (1986) pp. 101ff |
Subdifferential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subdifferential&oldid=14652