Morse function

A smooth function with certain special properties. Morse functions arise and are used in Morse theory.

Let be a smooth complete (in some Riemannian metric) Hilbert manifold (for example, finite dimensional) whose boundary is a disconnected union (possibly empty) of manifolds and . A Morse function for the triple is a smooth (of Fréchet class ) function , (or for ), such that:

1) , ;

2) all critical points (cf. Critical point) of 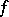lie in and are non-degenerate;

3) condition 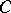of Palais–Smale is fulfilled (see [2], [3]). I.e. on any closed set where 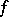is bounded and the greatest lower bound of 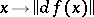is zero, there is a critical point of .

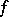For example, if 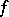is a proper function, that is, all sets 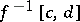, , 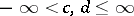are compact (possible only for ), then 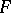satisfies condition 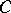. A Morse function attains a (global) minimum on each connected component o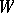f . If is a finite-dimensional manifold, then for the set of Morse functions of class is a set of the second category (and, if 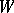is compact, even a dense open set) in the space of all functions

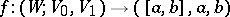in the -topology.

References

[1]	M. Morse, "The calculus of variations in the large" , Amer. Math. Soc. (1934)
[2]	R.S. Palais, "Morse theory on Hilbert manifolds" Topology , 2 (1963) pp. 299–340
[3]	S. Smale, "Morse theory and a nonlinear generalization of the Dirichlet problem" Ann. of Math. , 80 (1964) pp. 382–396

Comments

There exist generalizations to Morse functions on stratified spaces (cf. (the editorial comments to) Morse theory and [a1]) and to equivariant Morse functions (cf. [a2] and [a3]).

References

[a1]	M. Goreski, R. MacPherson, "Stratified Morse theory" , Springer (1988)
[a2]	A. Wasserman, "Morse theory for -manifolds" Bull. Amer. Math. Soc. , 71 (1965) pp. 384–388
[a3]	A. Wasserman, "Equivariant differential topology" Topology , 8 (1969) pp. 127–150