Convex integration
One of the methods developed by M. Gromov to prove the 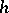 -principle. The essence of this method is contained in the following statement: If the convex hull of some path-connected subset
-principle. The essence of this method is contained in the following statement: If the convex hull of some path-connected subset 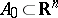 contains a small neighbourhood of the origin, then there exists a mapping
contains a small neighbourhood of the origin, then there exists a mapping 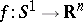 whose derivative sends
whose derivative sends 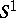 into
into 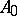 . This is equivalent to saying that the differential relation for mappings
. This is equivalent to saying that the differential relation for mappings 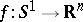 given by requiring
given by requiring 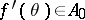 for all
for all 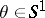 satisfies the
satisfies the 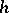 -principle. More generally, the method of convex integration allows one to prove the
-principle. More generally, the method of convex integration allows one to prove the 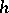 -principle for so-called ample relations
-principle for so-called ample relations 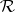 . In the simplest case of a
. In the simplest case of a 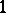 -jet bundle
-jet bundle 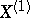 over a
over a 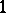 -dimensional manifold
-dimensional manifold 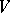 , this means that the convex hull of
, this means that the convex hull of 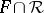 is all of
is all of 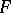 for any fibre
for any fibre 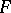 of
of 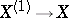 (notice that this fibre is an affine space). The extension to arbitrary dimension and higher-order jet bundles is achieved by studying codimension-one hyperplane fields
(notice that this fibre is an affine space). The extension to arbitrary dimension and higher-order jet bundles is achieved by studying codimension-one hyperplane fields  in
in 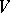 and intermediate affine bundles
and intermediate affine bundles 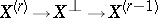 defined in terms of
defined in terms of  .
.
One particular application of convex integration is to the construction of divergence-free vector fields and related geometric problems.
References
| [a1] | M. Gromov, "Partial differential relations" , Ergebn. Math. Grenzgeb. (3) , 9 , Springer (1986) |
| [a2] | D. Spring, "Convex integration theory" , Monogr. Math. , 92 , Birkhäuser (1998) |
Convex integration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_integration&oldid=14622