Optimal quadrature

A quadrature formula giving the best approximation to the integral

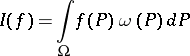for a class 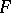of integrands. If

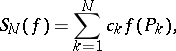then

is called the quadrature error when calculating the integral of a given function, while

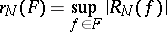is called the quadrature error in the class 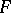. If a quadrature formula exists such that for the corresponding 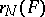the equality

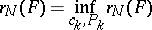holds, then this formula is called the optimal quadrature in this class.

Optimal quadratures have only been found for certain classes of functions which, basically, depend on one variable (see [1]–[3]). Optimal quadratures are also called best quadrature formulas or extremal quadrature formulas.

References

[1]	S.M. Nikol'skii, "Quadrature formulae" , H.M. Stationary Office , London (1966) (Translated from Russian)
[2]	N.S. Bakhvalov, "On optimal convergence estimates for quadrature processes and integration methods of Monte-Carlo type on function classes" , Numerical Methods for Solving Differential and Integral Equations and Quadrature Formulas , Moscow (1964) pp. 5–63 (In Russian)
[3]	S.L. Sobolev, "Introduction to the theory of cubature formulas" , Moscow (1974) (In Russian)

References

[a1]	H. Engels, "Numerical quadrature and cubature" , Acad. Press (1980)