Quasi-periodic function

with periods

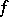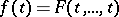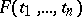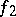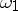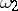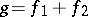A function such that for some continuous function of variables that is periodic with respect to with periods , respectively. All the are required to be strictly positive and their reciprocals have to be rationally linearly independent. If and are continuous periodic functions with periods and , respectively, where is irrational, then and 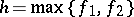are quasi-periodic functions.

The theory of quasi-periodic functions serves as a basis for the creation of the theory of almost-periodic functions (cf. Almost-periodic function). In the case of continuous functions, quasi-periodic functions are a generalization of periodic functions, but a particular case of almost-periodic functions.

Quasi-periodic functions have a representation

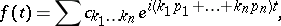where the 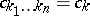are such that 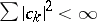. Quasi-periodic functions possess the following properties: addition and multiplication of quasi-periodic functions yield quasi-periodic functions; a sequence of quasi-periodic functions that is uniformly convergent for 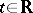gives in the limit an almost-periodic function; if 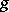is an almost-periodic function and 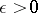, then there exists a quasi-periodic function 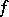such that

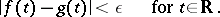References

[1]	P. Bohl, "Über die Darstellung von Funktionen einer Variabeln durch trigonometrische Reihen mit mehreren einer Variabeln proportionalen Argumenten" , Dorpat (1893) (Thesis)
[2]	V.Kh. Kharasakhal, "Almost-periodic solutions of ordinary differential equations" , Alma-Ata (1970) (In Russian)

Comments

Quasi-periodic functions of time occur naturally in Hamiltonian mechanics to describe multi-periodic motions of integrable systems (see [a1] and Quasi-periodic motion).

Consider Hill's differential equation

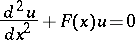(a1)

with periodic 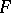, 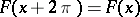. A particular case is Mathieu's differential equation

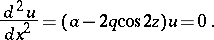(a2)

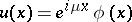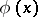A solution of (a1) need not be periodic. However, there is always a particular solution of the form with periodic (Floquet's theorem; cf. [a1] for a more precise statement). If the characteristic exponent 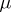is real, 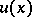is a quasi-periodic function.

References

[a1]	V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)
[a2]	P.G. Bohl, "Ueber eine Differentialgleichung der Störungstheorie" Crelles J. , 131 (1906) pp. 268–321
[a3]	B.M. Levitan, V.V. Zhikov, "Almost periodic functions and differential equations" , Cambridge Univ. Press (1984) pp. 47–48 (Translated from Russian)
[a4]	W. Magnus, S. Winkler, "Hill's equation" , Dover, reprint (1979) pp. 4ff