Biased estimator
A statistical estimator whose expectation does not coincide with the value being estimated.
Let  be a random variable taking values in a sampling space
be a random variable taking values in a sampling space  ,
,  , and let
, and let  be a statistical point estimator of a function
be a statistical point estimator of a function  defined on the parameter set
defined on the parameter set  . It is assumed that the mathematical expectation
. It is assumed that the mathematical expectation  of
of  exists. If the function
exists. If the function
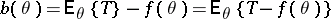 |
is not identically equal to zero, that is,  , then
, then  is called a biased estimator of
is called a biased estimator of  and
and  is called the bias or systematic error of
is called the bias or systematic error of 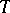 .
.
Example. Let  be mutually-independent random variables with the same normal distribution
be mutually-independent random variables with the same normal distribution 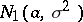 , and let
, and let
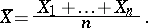 |
Then the statistic
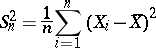 |
is a biased estimator of the variance 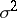 since
since
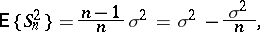 |
that is, the estimator  has bias
has bias 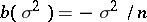 . The mean-square error of this biased estimator is
. The mean-square error of this biased estimator is
 |
The best unbiased estimator of 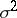 is the statistic
is the statistic
 |
with mean-square error
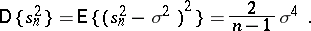 |
When  , the mean-square error of the biased estimator
, the mean-square error of the biased estimator  is less than that of the best unbiased estimator
is less than that of the best unbiased estimator  .
.
There are situations when unbiased estimators do not exist. For example, there is no unbiased estimator for the absolute value  of the mathematical expectation
of the mathematical expectation  of the normal law
of the normal law 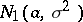 , that is, it is only possible to construct biased estimators for
, that is, it is only possible to construct biased estimators for 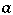 .
.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
Biased estimator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Biased_estimator&oldid=14599