Ordered sum

of partially ordered sets

An operation which associates with a system of disjoint partially ordered sets , where the index set is also partially ordered, a new partially ordered set

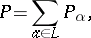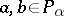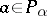the elements of which are the elements of the set-theoretical union of the sets , with order defined as follows. On the set one has if and only if either and in or , and 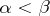. Important particular cases of ordered sums are the cardinal and ordinal sums. The first of these is obtained when 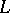is trivially ordered, i.e. each of its elements is comparable only to itself, and the second when 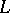is a totally ordered set. Thus, in the cardinal sum of two disjoint partially ordered sets and 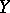the relation 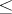retains its meaning in the components 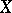and 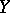, while 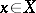and are incomparable; in the ordinal sum of 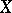and 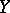the order relation is again preserved in the components and 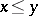for all , .

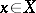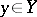References

[1]	G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973)
[2]	L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian)