Orthogonal basis
A system of pairwise orthogonal non-zero elements 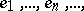 of a Hilbert space
of a Hilbert space 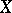 , such that any element
, such that any element 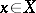 can be (uniquely) represented in the form of a norm-convergent series
can be (uniquely) represented in the form of a norm-convergent series
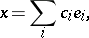 |
called the Fourier series of the element  with respect to the system
with respect to the system 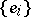 . The basis
. The basis 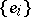 is usually chosen such that
is usually chosen such that 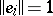 , and is then called an orthonormal basis. In this case, the numbers
, and is then called an orthonormal basis. In this case, the numbers 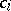 , called the Fourier coefficients of the element
, called the Fourier coefficients of the element  relative to the orthonormal basis
relative to the orthonormal basis 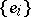 , take the form
, take the form 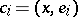 . A necessary and sufficient condition for an orthonormal system
. A necessary and sufficient condition for an orthonormal system 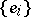 to be a basis is the Parseval–Steklov equality
to be a basis is the Parseval–Steklov equality
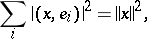 |
for any 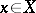 . A Hilbert space which has an orthonormal basis is separable and, conversely, in any separable Hilbert space an orthonormal basis exists. If an arbitrary system of numbers
. A Hilbert space which has an orthonormal basis is separable and, conversely, in any separable Hilbert space an orthonormal basis exists. If an arbitrary system of numbers 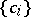 is given such that
is given such that 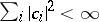 , then in the case of a Hilbert space with a basis
, then in the case of a Hilbert space with a basis 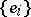 , the series
, the series 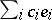 converges in norm to an element
converges in norm to an element 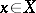 . An isomorphism between any separable Hilbert space and the space
. An isomorphism between any separable Hilbert space and the space 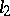 is established in this way (Riesz–Fischer theorem).
is established in this way (Riesz–Fischer theorem).
References
| [1] | L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Wiley & Hindustan Publ. Comp. (1974) (Translated from Russian) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Pitman (1981) (Translated from Russian) |
| [3] | N.I. [N.I. Akhiezer] Achieser, I.M. [I.M. Glaz'man] Glasman, "Theorie der linearen Operatoren im Hilbert Raum" , Akademie Verlag (1958) (Translated from Russian) |
Comments
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
Orthogonal basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_basis&oldid=14572