Choquet simplex

A non-empty compact convex set in a locally convex space that possesses the following property: Under the imbedding of as the hyperplane in the space the projecting cone

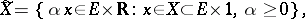of transforms the space into a partially ordered space for which the space generated by , which is the space of differences , is a lattice. In the case when is finite-dimensional, a Choquet simplex is an ordinary simplex with number of vertices equal to . There exists a number of equivalent definitions of a Choquet simplex (see [1]). One of them reduces to the requirement that an intersection of with any translate of 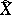should be again a translate of .

When, in addition to the above requirements, 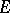is separable and 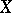is metrizable, then for 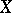to be a Choquet simplex it is necessary and sufficient that any point is the centre of gravity of the unique measure concentrated at the extreme points of . The concept of a Choquet simplex is essential when studying the uniqueness of an integral representation of a function (see [1], [2]). It was introduced by G. Choquet.

References

[1]	R.R. Phelps, "Lectures on Choquet's theorem" , v. Nostrand (1966)
[2]	E.M. Alfsen, "Compact convex sets and boundary integrals" , Springer (1971)

Comments

The Choquet unique representation theorem says that a compact convex metrizable subset of a locally convex space is a Choquet simplex if and only if for each 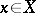there exists a unique measure 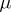concentrated on the extremal points of 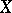which represents (i.e. has as "centre of gravity" ).